The 80-80-20 Triangle Problem, A Derivative, Solution #9

$ABC\;$ is an isosceles triangle with vertex angle $\angle BAC = 20^{\circ}\;$ and $AB = AC.\;$ Point $E\;$ is on $AB\;$ such that $AE = BC.\;$ Find the measure of $\angle AEC.$

Solution

This solution is by Miguel, Ochoa Sanchez, Peru.

Construct an equilateral $\Delta ABD.$

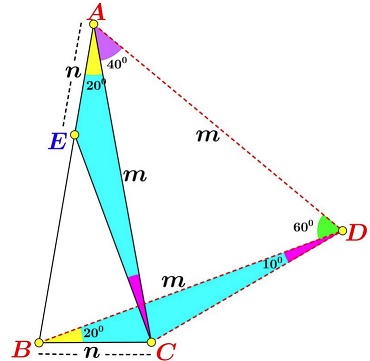
Since $AC=AB=AD,\;$ $\Delta CAD\;$ is isosceles, implying $\angle ACD=\angle ADC=70^{\circ}.$

Further, by SAS, $\Delta EAC=\Delta CBD$ so that $\angle ECA=\angle CDB=10^{\circ}.$ Thus $\angle AEC=\angle BCD=150^{\circ}.$

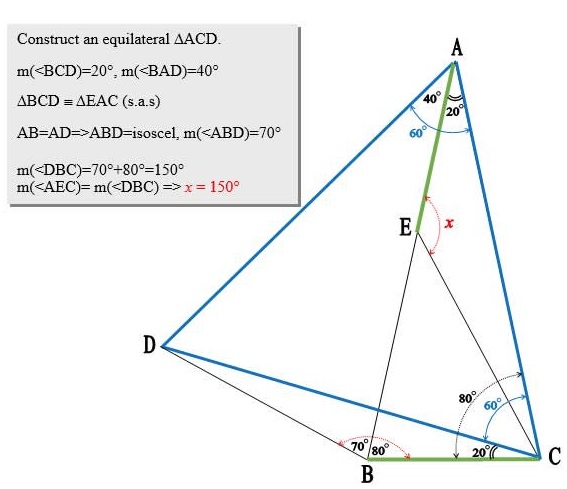
Here's a variant by Silvia Doandes, a pww:

a variant of a 80-80-20 problem

73324497