The 80-80-20 Triangle Problem, A Derivative, Solution #8

$ABC\;$ is an isosceles triangle with vertex angle $\angle BAC = 20^{\circ}\;$ and $AB = AC.\;$ Point $E\;$ is on $AB\;$ such that $AE = BC.\;$ Find the measure of $\angle AEC.$

Solution

This solution is by John Rhodes, a maths teacher at the Woodhouse sixth form college, London, UK, and independently by a student of his Sajida Ali.

Consider an isosceles $\Delta ACD,\;$ with $\angle ACD=20^{\circ}$ and $AC=CD.\;$ Form an equilateral $\Delta ADE$ within $\Delta ACD.\;$ Join $E$ to $C.\;$ Observe that $\angle AEC=150^{\circ}.$

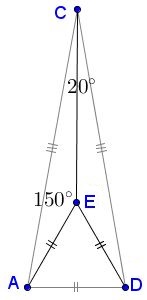
Extend now $AE\;$ beyond $E$ to $B;$ so as to have $\angle ABC=80^{\circ}.$

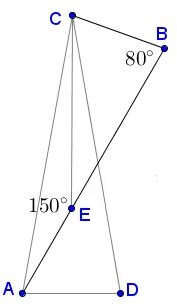
By chasing angles, $\angle BDC=50^{\circ},\;$ $\angle BEC=30^{\circ},\;$ $\angle BCE=70^{\circ},\;$ $\angle ACB=80^{\circ},$ making $\Delta ABC$ isosceles, with $\angle BAC=20^{\circ}.$

Further, $AB=AC=CD$ so that triangles $ACD$ and $BAD$ are congruent by SAS, making $BC=AD=AE.$

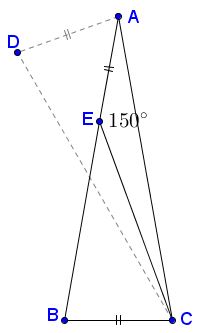
Finally, rotate $\Delta ABC$ into the proper position:

71568655