The 80-80-20 Triangle Problem, A Derivative, Solution #7

ABC is an isosceles triangle with vertex angle ∠BAC = 20° and AB = AC. Point E is on AB such that AE = BC. Find the measure of ∠AEC.

Solution

This solution has been reported in [Which Way Did the Bicycle Go?].

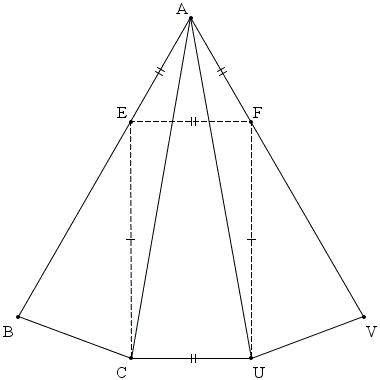
Add a couple of triangles ACU and AUV equal to ΔABC and mark point F on AV, AF = AE. ∠EAF = 60° which makes ΔEAF equilateral. Thus, EF = AE = BC = CU. Also, because of the symmetry, EF||CU so that CEFU is a parallelogram. And again, with a nod to the symmetry, the angles CEF and UFE are right, and so are the angles ECU and FUC. Importantly, ∠ECU = 90°. This solves the problem:

∠ACE = ∠ECU - ∠ACU = 90° - 80° = 10°,
∠AEC = 180° - 20° - 10° = 150°.

Reference

J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #15

71536043