The 80-80-20 Triangle Problem, A Derivative, Solution #5
ABC is an isosceles triangle with vertex angle |Contact| |Front page| |Contents| |Geometry| |Up| |Store| Copyright © 1996-2012 Alexander Bogomolny This solution has been reported in [Leikin]. It applies the same strategy as Solution #5, viz., assuming ∠ACE = 10° and subsequently proving that Form ΔACS congruent to ΔABC:
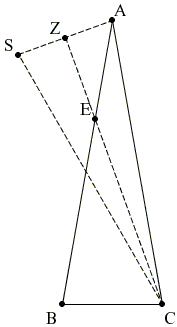
Since ∠ACE = 10°, CE serves as an angle bisector in the isosceles ΔACS. Hence, it is also the altitude and the median from C. Let Z be its foot, the midpoint of AS. We have
But in right ΔAEZ, ∠EAZ = 60° which makes So indeed ∠ACE = 10° and ∠AEC = 150°. Reference|Contact| |Front page| |Contents| |Geometry| |Up| |Store| Copyright © 1996-2012 Alexander Bogomolny |
| 40617828 |
