ABC is an isosceles triangle with vertex angle BAC = 20° and AB = AC. Point E is on AB such that AE = BC. Find the measure of AEC.

Solution

Copyright © 1996-2010 Alexander Bogomolny

The solution is based on embedding the diagram into a regular 18-gon.

Line CE appears to pass through vertex X of the 18-gon, with CAX = 160°. Instead of showing this, we'll join vertex X to C and prove that the intersection L of CX with AB coincides with E.

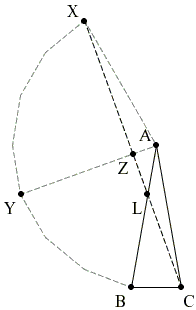
Let Y be the vertex of the 18-gon, midway between X and C and Z the foot of the perpendicular from A to CX, i.e. the intersection of CX with AY. Since ΔACX is isosceles, CAZ = CAX / 2 = 80°. In the right ΔALZ, LAZ = 80° - 20° = 60° meaning ΔALZ is a 30-60-90 triangle with AL = 2·AZ. In order to show that AL = BC we have to show that BC = 2·AZ or, if M is the midpoint of BC, that AZ = MC.

To see that this is so draw AM and consider two right triangles, ACZ and ACM. These are equal by ASA: they share side AC and both have 80° angles.

We conclude that indeed L coincides with E, from which

ECA = LCA = CAM = 10°.

And finally, AEC = 180° - 10° - 20° = 150°.

Reference

1. R. Honsberger, Mathematical Chestnuts from Around the World, MAA, 2001, Ch 2.

Copyright © 1996-2010 Alexander Bogomolny