The 80-80-20 Triangle Problem, A Derivative, Solution #2
| |
ABC is an isosceles triangle with vertex angle  BAC = 20° and AB = AC. Point E is on AB such that AE = BC. Find the measure of AEC.
|
Solution
Copyright © 1996-2008 Alexander Bogomolny
The solution is by Ian McGee of the University of Waterloo.
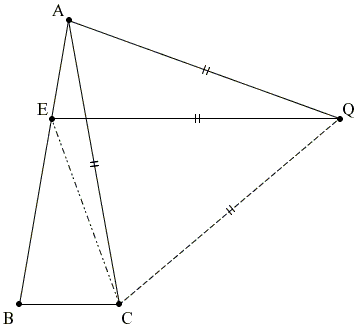
Construct an isosceles triangle AEQ with AQE = 20°. Since. AE = BC, the latter is equal to ΔABC. In particular, AQ = AC. Also,
| |
CAQ = EAQ - EAC = 80° - 20° = 60°.
|
Which makes ΔACQ equilateral. In particular, CQ = EQ = AQ.
In ΔCQE, EQ = CQ and CQE = 60° - 20° = 40°. Thus, CEQ = (180° - 40°) / 2 = 70° so that AEC = 80° + 70° = 150°.
Reference
- R. Honsberger, Mathematical Chestnuts from Around the World, MAA, 2001, Ch 2.
Copyright © 1996-2008 Alexander Bogomolny
|
