Pythagorean Theorem from the Shoelace Formula

John Molokach also observed that the Pythagorean theorem follows from Gauss' Shoelace Formula. The formula gives the area of a polygon A₁A₂...A_n in the Cartesian plane, where vertices are defined by their coordinates, A_j = (x_j, y_j), j = 1, ..., n:

Area(A₁A₂...A_n) = ½|∑(x_jy_j+1 - x_j+1y_j)| = ½|∑x_j(y_j+1 - y_j-1)|,

where the sum is taken for j = 1, ..., n and the indices are defined cyclically: x_n+1 = x₁ and x₀ = x_n and similarly for y's.

For the square with vertices A₁(b, 0), A₂(a+b, b), A₃(a, a+b), A₄(0, a), the formula gives

PT from Gauss' Shoelace formula

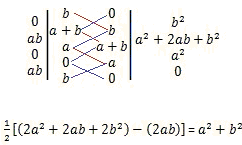
On the other hand, if c is the hypotenuse of the right triangle with vertices (0, 0), (b, 0), and (0, a) then the area of the square formed on the hypotenuse is c², showing that indeed a² + b² = c².

A question could be asked whether the Shoelace formula, in itself, is based on the Pythagorean theorem, causing a vicious circle in proving the latter. Eschewing this question for the time being, we present Roger Nelsen's synthetic proof without words that algebraically is equivalent to the above derivation:

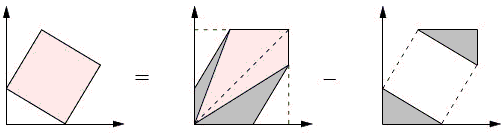
PT from Gauss' Shoelace formula. Roger Nelsen's synthetic illustration

In the first figure on the right, one of the darker triangles has area a²/2, the other one - b²/2. The light triangles have areas a(a + b)/2 and b(a + b)/2, giving together (a + b)²/2. Each of the triangles in the right figure has area of ab/2. This we get, for the area of the square c×c on the left

a²/2 + b²/2 + (a + b)²/2 - 2ab/2 = a² + b².

71927381