Pythagorean Theorem by Contradiction
Problem

Proof
Let $h$ be the altitude from the right angle. The right triangle $(a,b,c)$ is split into two triangles, $(x,h,a)$ and $(h,y,b),$ both similar to the triangle $(a,b,c).$ In particular, $h^2=xy.$
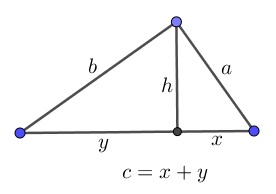
Assume to the contrary that $a^2+b^2\ne c^2.$ Let, e.g, $a^2+b^2\lt c^2.$ Then, by similarity, also
$x^2+h^2\lt a^2$ and $h^2+y^2\lt b^2.$
Summing up yields a contradiction:
$\begin{align}a^2+b^2\,&\gt (x^2+h^2)+(h^2+y^2)=x^2+y^2+2h^2\\ &=x^2+y^2+2xy=(x+y)^2=c^2, \end{align}$
so that $a^2+b^2\gt c^2,$ contrary to our assumption.
Acknowledgment
The proof by K. B. SUBRAMANIAM, Math. Gaz. 102 (2018) p. 128 was kindly pointed to me by Grégoire Nicollier.
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579145
