Hypocycloids

Here I wish to consider a special case of hypocycloids where the radius r of the rolling circle k is exactly half that of the fixed circle K, r = R/2. We shall assume that there is no slipping and look into two situations:

the tracing point lies on the rolling circle
the tracing point lies inside the rolling circle

Proposition 1

Hypocycloids with r = R/2 degenerate into diameters of K.

Proof

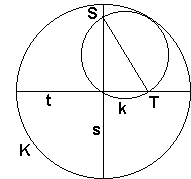
Consider two positions k and k₁ of the rolling circle. Point P₁ on k₁ corresponds to the point P where the small circle k touched K. Let M and m₁ be the centers of the circles K and k₁, respectively. Let Q be the point of contact between K and k₁.

Since the circles roll without slipping, the arc QP₁ of k₁ is congruent with the arc QP of k. Furthermore, since k is half the size of K, it follows that ∠Qm₁P₁ = 2∠QMP, and in addition that M lies on k₁. Hence we have, by the well-known theorem about the angles subtended at the circumference and at the center of a circle, that ∠QMP₁ = (1/2)∠Qm₁P₁ = ∠QMP. Hence the straight line MP₁ coincides with MP, i.e. P₁ travels on the straight line MP during the course of the motion.

That P has been chosen as the point where two circles K and k touch is absolutely immaterial. In the course of the motion any point on k sooner or later will touch K. Therefore, our argument would apply to that point as well.

Proposition 2

Hypotrachoids with r = R/2 degenerate into ellipses.

Proof

In the process of rolling, the arc ST, where S and T are the two ends of a diameter of k, corresponds to one quarter of the circumference of K. Therefore, by Proposition 1, S and T move on two perpendicular diameters, s and t, of K. Changing the viewpoint, this is exactly the case of a ladder sliding off a wall, the problem we considered elsewhere.

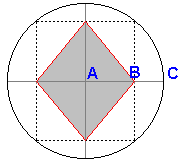
One related problem

In the middle of a city park there is a large circular playing area. The city council would like to put a diamond shaped wading pool inside the circular area. It's known that AB = 6 and BC = 3. What is the side of the diamond?

More of hypocycloids

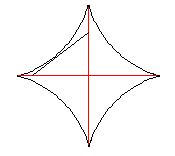
You may have noticed that all hypocycloids (unlike hypotrachoids) have cusps. The number of cusps is equal to the ratio of the two radii provided that the ratio is integer. In case of three cusps, the segment of the tangent which is inside the curve has constant length irrespective of its position.

The hypocycloid with four cusps is called astroid. If we restrict ourselves to segments of tangents cut by the two perpendicular axes of symmetry then a similar property will hold - these segments have constant length. Both statements stem from the Two-circles theorem [Lines and Curves, 153-154]:

Let two circles - one of radius twice that of the other - roll over the same curve always staying in touch. Suppose that the (fixed) diameter KL of the bigger circle was chosen such that at the start point K and point M on the smaller circle both coincided with a point on the curve. Then KL is tangent to the trajectory of point M.

References

D. Hilbert and S. Cohn-Vossen, Geometry and Imagination, Chelsea Publishing Co, NY 1990.
V. Gutenmacher, N. Vasilyev, Lines and Curves: A Practical Geometry Handbook , Birkhauser; 1 edition (July 23, 2004)

71536493