Pythagorean Perimeter Theorem
The problem due to Miguel Ochoa Sanchez has been posted at the CutTheKnotMath facebook page along with a solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.
Source
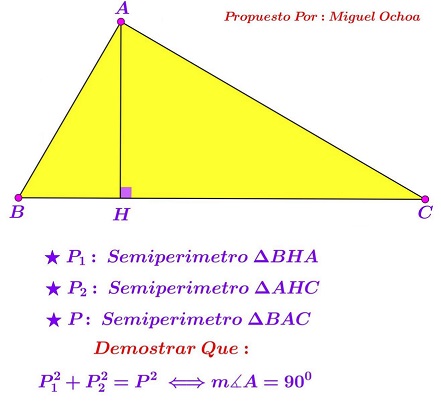
Problem
Point $H$ is the foot of the altitude in $\Delta ABC$ to the side $BC.$
Let $p(\Delta )$ be the perimeter of triangle $\Delta.\;$ Prove that
$\left(p(ABH)\right)^2+\left(p(ACH)\right)^2=\left(p(ABC)\right)^2$
iff $\angle BAC=90^{\circ}.$
Proof
We choose $H=(0,0),$ $A=(0,1),$ $B=(-b,0),$ $C=(c,0),$ with $b,c\gt 0.$ We have $BH=b,$ $CH=c,$ $AH=1,$ $BC=b+c,$ $AB=\sqrt{b^2+1},$ $AC=\sqrt{c^2+1}.$ We need to prove that the condition $AC\perp AB$ is equivalent to
$\left[1+\left(b+\sqrt{b^2+1}\right)\right]^{2}+\left[1+\left(c+\sqrt{c^2+1}\right)\right]^{2}=\left[\left(b+\sqrt{b^2+1}\right)+\left(c+\sqrt{c^2+1}\right)\right]^{2}.$
The latter is transformed into
$1+2\left(b+\sqrt{b^2+1}\right)+1+2\left(c+\sqrt{c^2+1}\right)=2\left(b+\sqrt{b^2+1}\right)\left(c+\sqrt{c^2+1}\right),$
or,
$1+\left(b+\sqrt{b^2+1}\right)+\left(c+\sqrt{c^2+1}\right)=\left(b+\sqrt{b^2+1}\right)\left(c+\sqrt{c^2+1}\right).$
Introduce $x,y\gt 1$ such that $\displaystyle b=\frac{x^2-1}{2x}\;$ and $\displaystyle c=\frac{y^2-1}{2y}.\;$ Then $b+\sqrt{b^2+1} = x\;$ and $c+\sqrt{c^2+1}=y.\;$ So that the identity at hand becomes $1+x+y=xy.$
To make it clear, the problem has been reduced to showing that the condition $AC\perp AB$ is equivalent to $1+x+y=xy.$ This is indeed so, because $AC\perp AB$ is equivalent to $bc=1$ which, in turn, is equivalent to $(x^2-1)(y^2-1)=4xy,$ and this is algebraically manipulated into $(xy-1)^2=(x+y)^2.$ Since $x,y\gt 1,\;$ $xy-1=x+y,$ as required.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581992
