Pythagorean Theorem via the Area Determinant

This is a well known fact in linear algebra that a \(2\times 2\) determinant \(\left| \begin{array}{cc} a & b \\ c & d \end{array} \right| = ad - bc\) defines the signed area of the parallelogram on two vectors \(\left( \begin{array}{c} a \\ c \end{array} \right)\) and \(\left( \begin{array}{c} b \\ d \end{array}\right)\).

John Molokach applied that property of determinants to the following diagram:

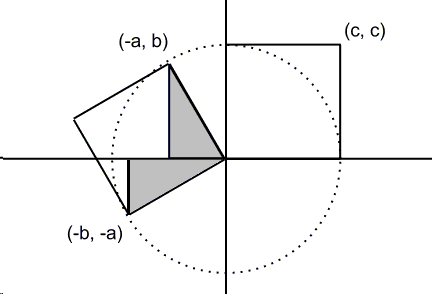
a proof of the pythagorean theorem based on the area determinant formula. By John Molokach

There are two squares with side \(c\) and area \(c^{2}\). One of them is identified as a parallelogram on vectors \(\left( \begin{array}{c} -a \\ b \end{array} \right)\) and \(\left( \begin{array}{c} -b \\ -a \end{array} \right)\). The area of the parallelogram is expressed as \(|(-a)(-a)-b(-b)|=a^{2}+b^{2}\). Since the two areas are equal, \(c^{2}=a^{2}+b^{2}\), the Pythagorean theorem.

John accompanied his diagram by a telling formula:

\( \Bigg|\left| \begin{array}{cc} c & 0 \\ 0 & c \end{array} \right|\Bigg| = \Bigg|\left| \begin{array}{cc} -a & b \\ -b & -a \end{array} \right|\Bigg| \)

71940142