Pythagorean Theorem by Stretching
What Is This About?
Make a Guess
Problem
Given a rectangle with sides $a,b$ and the diagonal $c:$
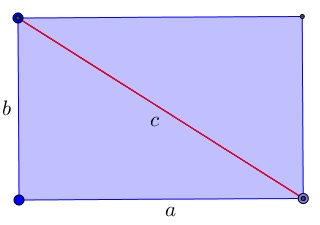
Then $a^2+b^2=c^2.$
Proof
This unconventional proof may be done with a little of calculus or without; I find it strikingly charming. The proof (by Andrew Stacey) is based on the following diagram
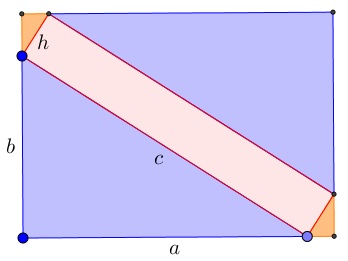
The starting point is a rectangle with sides $a,b$ and the diagonal $c:$

Clearly we intend to show that $a^2+b^2=c^2.$ By cutting the given rectangle along the diagonal and shifting the two halves in the direction perpendicular to the diagonal we obtain the diagram we displayed at the outset:

The big rectangle consists of five pieces: two blue triangles of combined area $ab;$ two orange triangles of combined area $\displaystyle \frac{ah}{c}\cdot\frac{bh}{c}=\frac{abh^2}{c^2};$ a rectangle of area $ch.$ The sides of the outer rectangle are $\displaystyle a+\frac{bh}{c}$ and $\displaystyle b+\frac{ah}{c}.$ By computing its area in two ways we get
$\displaystyle\left(a+\frac{bh}{c}\right)\left(b+\frac{ah}{c}\right)=ab+ch+\frac{abh^2}{c^2}.$
Now open the parentheses and cancel similar terms:
$\displaystyle \frac{a^2+b^2}{c}=c,$
i.e., the Pythagorean identity.
Note that it is also possible to invoke a little calculus. Rewrite the identity of the areas as
$\displaystyle\left(a+\frac{bh}{c}\right)\left(b+\frac{ah}{c}\right)=ab+ch+O(h^2),$
with the $big-O$ term. This leads to
$\displaystyle \frac{a^2+b^2}{c}h=ch+O(h^2),$
or $\displaystyle \frac{a^2+b^2}{c}=c+O(h),$ where passing to the limit as $h\to 0$ delivers the same Pythagorean identity.
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73588115
