Pythagorean Theorem through Equilateral Triangles
What follows is an excerpt from a April 12, 2016 paper by Andrés Navas (Dpto. de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile). It gives justification to Euclid V.31 without a recourse to similarity of triangles. The proof employs equilateral triangles, the one on the hypotenuse with the different orientation than those on the legs of a right triangle. This is reminiscent of the usage of squares in Proofs 24, 63, and 69.
The proof is based on the following diagram:
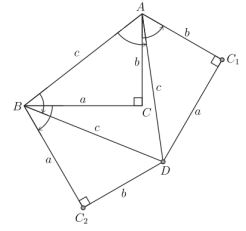
which was obtained in the following manner: Rotate the given $\Delta ABC\;$ counterclockwise through $60^{\circ}\;$ at the vertex $A,\;$ and clockwise also in $60^{\circ}\;$ at $B.\;$ Call $C_1,\;$ $B_1\;$ and $C_2,\;$ $A_2\;$ the image of the vertices, as shown above. Notice that $BA_2 = c = AB_1\;$ and $\angle ABA_2 = \angle BAB_1 = 60^{\circ}.\;$ Hence, $A_2\;$ and $B_1\;$ coincide, and denoting this point by $D,\;$ the vertices $A,\;$ $B\;$ and $D\;$ determine an equilateral triangle of side length $c.$
Also, notice that $BCC_2\;$ and $ACC_1\;$ are equilateral triangles of side length $a\;$ and $b,\;$ respectively. Moreover, triangles $BC_2D\;$ and $AC_1D\;$ are both congruent to triangle $BCA.$
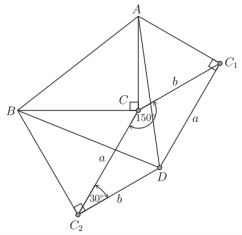
Now, referring to the areas, we have
$\begin{align} ABC_2DC_1 &= ABD + BC_2D + AC_1D\\ & = ACC_1 + BCC_2 + BCA + C_2DC_1C. \end{align}$
In pictures:
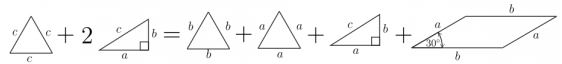
which yields
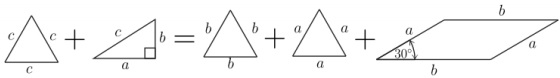
We are hence left to prove that
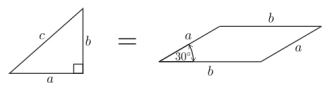
To do this, note that $C_2DC_1C\;$ is a parallelogram of sides $a\;$ and $b.\;$ Besides, as $\angle BCA = 90^{\circ},\;$ we have that $\angle C_1CC_2\;$ must equal $120^{\circ},\;$ hence $\angle CC_2D = \angle DC_1C = 30^{\circ}.\;$ Thus, the area of $C_1CC_2D\;$ equals $ab\sin(30^{\circ})=\frac{1}{2}ab\;$ which is the area of $\Delta BCA,\;$ as desired.
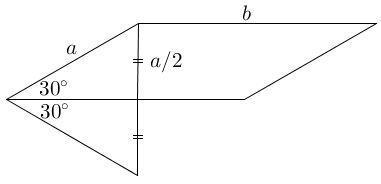
Remark. In the last step above, one can certainly avoid the use of trigonometry by just looking at the picture below ...
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608402
