Pythagorean Theorem, Proof 114

Bùi Quang Tuán
Submitted March 1, 2015

The proof is based on the following diagram:

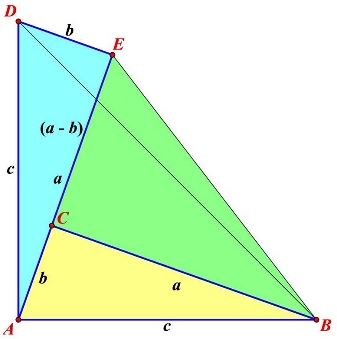
Pythagorean theorem, proof 114

$ABC$ is a triangle right at $C,$ with three side lengths $a,$ $b,$ $c.$ Construct triangle $ADE$ congruent with $ABC$ such that $AD\perp AB$ and $E$ is on the ray $AC.$ Let $[X]$ denote the area of $X.$ We calculate $[ABED]$ in two ways.

$[ABED] = [ABC] + [ADE] + [BCE] = ab/2 + ab/2 + (a - b)a/2$

and

$[ABED] = [ABD] + [BDE]= c^2/2 + (a - b)b/2$

From (1) and (2):

$2ab + (a - b)a = c^2 + (a - b)b$

which is easily simplified to $a^2+b^2=c^2.$

71867281

Pythagorean Theorem, Proof 114

Bùi Quang Tuán Submitted March 1, 2015

Bùi Quang Tuán
Submitted March 1, 2015