Pythagorean Theorem by Inscribed Semicircle

J. Molokach
Submitted May 19, 2015

The theorem is ilustrated in figure below.

$a^2+b^2=c^2$

Pythagorean theorem

Inscribe a semicircle into the right triangle:

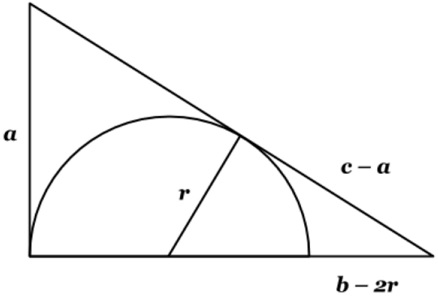
Pythagorean theorem, semicircle

To do that we only need to find the radius $r$ of the semicircle. This is determined from the proportion (due to the similarity of two triangles), $\displaystyle\frac{r}{c-a}=\frac{a}{b},$ so that $\displaystyle r=\frac{a(c-a)}{b}.$

To prove the Pythagorean theorem apply the Intersecting Chords Theorem: $(c-a)^{2}=b(b-2r).$ From this identity too we may express $\displaystyle r=\frac{b^{2}-(a-c)^{2}}{2b}.$ Comparing the two expressions for $r$ gives $2a(c-a)=b^{2}-(a-c)^{2}$ which is easily simplified to $a^2+b^2=c^2.$

71536646

Pythagorean Theorem by Inscribed Semicircle

J. Molokach Submitted May 19, 2015

J. Molokach
Submitted May 19, 2015