Pythagorean Theorem by Analytic Geometry
Nuno Luzia
Universidade Federal do Rio de Janeiro,
Instituto de Matemática
Rio de Janeiro 21941-909, Brazil
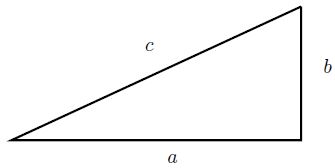
The theorem is ilustrated in figure below.
$a^2+b^2=c^2$
The figure below is obtained by putting another right triangle (marked with dotted line) on top of the original one, so as to form a rectangle with sides with lengths $a$ and $b$, and then reflecting it through the common hypotenuse.
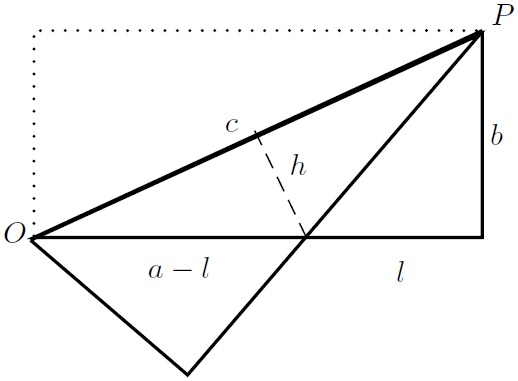
We get an isosceles triangle with base length $c$ and height $h$, and two smaller right rectangles with sides of lengths $l$, $b$ and $a-l,$ for some $l.$
The area of the isosceles triangle is equal to the area of the original triangle minus the area of one smaller right rectangle. So
(1)
$ch=b(a-l).$
(This equation can also be obtained by using a similarity between two right rectangles.)
We will determine $h$ and $l$ by using cartesian coordinates and basic vector calculus. We put the origin $O$ on the left corner of the original triangle, with the usual $x$ and $y$ axis for the cartesian coordinates. In this way, the vector $\vec{OP}$ along the hypotenuse is represented by the coordinates $(a,b)$.
To determine $h$ and $l$ we should find an orthogonal vector to $(a,b)$. Geometrically, changing the roles of $x$ and $y$ axis corresponds to a rotation of $90^\circ$ followed by a reflection through the horizontal axis, so the vector $(b,-a)$ is orthogonal to $(a,b)$.
Then the straight line segment starting at the midpoint of $OP$ and orthogonal to it is represented by
$(a/2, b/2)+t (b,-a),\quad t\ge 0.$
The $y$ coordinate of expression above is zero when $\displaystyle t=\frac{b}{2a}$, and then the $x$ coordinate is $\displaystyle \frac{a}{2}+\frac{b^2}{2a}$. So
(2)
$\displaystyle a-l=\frac{a}{2}+\frac{b^2}{2a}.$
Now $h$ is the length of $\displaystyle \frac{b}{2a} (b,-a)$ which is the length of $\displaystyle \frac{b}{2a} OP$. So
(3)
$\displaystyle h=\frac{b}{2a} c.$
(This equation can also be obtained by using a similarity between two right rectangles.)
Putting (2) and (3) into (1) we obtain the Pythagorean relation.
(Note that the validity of using calculus, let alone analytic geometry, to prove the Pythagorean theorem has been argued elsewhere.)
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579180
