Pythagorean Theorem via Half-Angle Formulas
Nuno Luzia
Universidade Federal do Rio de Janeiro,
Instituto de Matemática
Rio de Janeiro 21941-909, Brazil
Only very recently a trigonometric proof of the Pythagorean theorem was given by Zimba, many authors thought this was not possible. In this note we give other trigonometric proofs of the Pythagorean theorem by establishing, geometrically, the half-angle formula $\displaystyle \cos\theta=1-2\sin^2 \frac{\theta}{2}$.
The theorem is ilustrated in figure below.
$a^2+b^2=c^2$
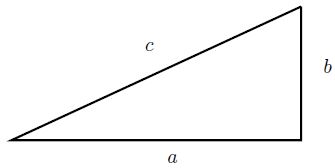
To prove this theorem it is enough to consider the particular case $c=1$, for then the general case follows by rescaling. Define the trigonometric functions $\sin \theta$ and $\cos \theta$, for $0\lt\theta\lt 90^\circ$, as usual:
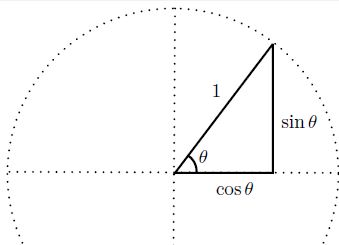
Then the Pythagorean theorem is equivalent to
(1)
$\cos^2 \theta + \sin^2 \theta=1,$
for every $0\lt\theta\lt 90^\circ$.
The subtraction formulas
$\begin{align} \cos(\alpha-\beta) &=\cos\alpha\cos\beta+\sin\alpha\sin\beta,\\ \sin(\alpha-\beta) &=\sin\alpha\cos\beta-\cos\alpha\sin\beta, \end{align} $
valid for $0\lt\alpha,\beta,\alpha-\beta\lt 90^\circ$, can be proved geometrically without using the Pythagorean theorem (see [Zimba]) who used these formulas to prove the Pythagorean theorem.
The addition formula
$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta,$
$0\lt\alpha,\beta,\alpha+\beta\lt90^\circ$, can, in the same way, also be proved geometrically without using the Pythagorean theorem, and, as a consequence, we get the half-angle formula
(2)
$\displaystyle \cos\theta=\cos^2 \frac{\theta}{2}-\sin^2\frac{\theta}{2}$
independent of the Pythagorean theorem. Substituting the Pythagorean formula (1) into (2) we get
(3)
$\displaystyle \cos\theta=1-2\sin^2 \frac{\theta}{2}.$
What if we could prove (3) without using the Pythagorean theorem? Then using (2) and (3) we would get the Pythagorean formula (1)!
Proof of half-angle formulas
First we observe the simple fact that in an isosceles triangle with two equal sides with length $1,$ forming an angle $\theta$, the length of the other side is $\displaystyle 2\sin\frac{\theta}{2}$. This can be seen by dividing the isosceles triangle in two right triangles with an angle $\displaystyle \frac{\theta}{2}:$
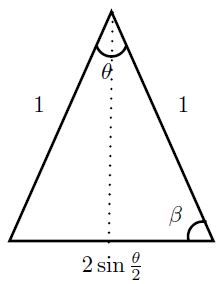
Also the other angles $\beta$ of the isosceles triangle satisfy $\theta+\beta+\beta=180^\circ$ or $\displaystyle \beta=90^\circ-\frac{\theta}{2}$. Of course, by definition, $\cos (90^\circ-\theta)=\sin\theta$ and $\sin (90^\circ-\theta)=\cos\theta$.
Now consider the two right triangles as in figure below, which together form an isosceles triangle as before:
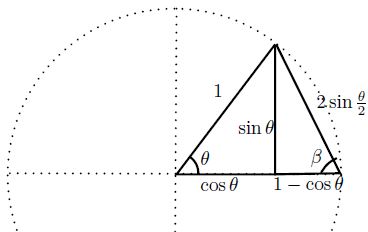
Using the trigonometric relations for the right hand side triangle, we get
$\begin{align*}\displaystyle 1-\cos\theta&=2\sin\frac{\theta}{2}\cos(90^\circ-\frac{\theta}{2}),\\ \sin\theta&=2\sin\frac{\theta}{2} \sin(90^\circ-\frac{\theta}{2}), \end{align*}$
or
(4)
$\displaystyle \cos\theta =1-2\sin^2\frac{\theta}{2},$ and
(5)
$\displaystyle \sin\theta =2\sin\frac{\theta}{2} \cos\frac{\theta}{2}.$
As mentioned before, (2) together with (3) imply the Pythagoras formula (1).
Another proof
Here we prove the the Pythagorean theorem using formulas (4) and (5) (instead of using formulas (3) and (1). We get
$\begin{align}\displaystyle \cos^2 \theta + \sin^2\theta &=\bigg(1-2\sin^2\frac{\theta}{2}\bigg)^{2}+\bigg(2\sin\frac{\theta}{2} \cos\frac{\theta}{2}\bigg)^{2}\\ &=1+4\sin^2\frac{\theta}{2} \left( \cos^2\frac{\theta}{2}+\sin^2\frac{\theta}{2}-1\right). \end{align}$
By mathematical induction we get
(6)
$\displaystyle \cos^2 \theta + \sin^2\theta=1+4^n\left(\prod_{i=1}^n\sin^2\frac{\theta}{2^i}\right) \left( \cos^2\frac{\theta}{2^n}+\sin^2\frac{\theta}{2^n}-1\right),$
for every natural number $n$. Clearly $\displaystyle \left| \cos^2\frac{\theta}{2^n}+\sin^2\frac{\theta}{2^n}-1\right|\le 1$ (actually this quantity can be made arbitrarly small by making $n$ large). Let $\theta$ be measured in radians. It follows from a figure above that $\displaystyle \sin\theta<2\sin\frac{\theta}{2}<\theta$. Then
$\displaystyle 4^n\prod_{i=1}^n\sin^2\frac{\theta}{2^i}<(4\theta^2)^n 4^{-\sum_{i=1}^n i} < (4\theta^2)^n 2^{-n^2},$
which is clearly arbitrarly small by making $n$ large enough. Then (6) implies the Pythagoras formula (1).
References
- J. Zimba, On the Possibility of Trigonometric Proofs of the Pythagorean Theorem, Forum Geometricorum, Volume 9 (2009) 275-278.
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73597543
