Another Algebraic Proof of the Pythagorean Theorem

This proof has been communicated to me by Marcelo Brafman (Israel).

The proof is based on the following diagram:

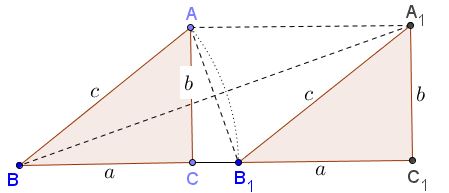
proof 102 of the Pythagorean theorem

The right $\Delta ABC$ is shifted along one of its legs $(BC$ in the diagram) through the distance equal to the lengths of the hypotenuse to the new position $A_{1}B_{1}C_{1}.$ In usual notation we have $BC=B_{1}C_{1}=a,$ $AC=A_{1}C_{1}=b,$ $AB=BB_{1}=A_{1}B_{1}=c.$ In particular, we obtain a rhombus $BB_{1}A_{1}A$ with sides equal to $c.$ The diagonals $AB_{1}$ and $BA_{1}$ are perpendicular, causing $\angle CAB_{1}=\angle A_{1}BC_{1}.$ Thus, the right triangles $CAB_{1}$ and $A_{1}BC_{1}$ are similar, from which

$\displaystyle\frac{AC}{B_{1}C}=\frac{BC_{1}}{A_{1}C_{1}}$ or $\displaystyle\frac{b}{c-a}=\frac{c+a}{b},$

the latter is equivalent to $c^{2}-a^{2}=b^{2}$ - the Pythagorean theorem.

71536305