Pythagorean Theorem via Geometric Progression

John Arioni has come with a derivation of the Pythagorean theorem that depends on the convergence of the geometric series. With the establishment of the fact that the Calculus of one variable could be (and, in fact, usually is) developed without invoking the Pythagorean theorem, it becomes clear that using the theory of limits in one variable to derive the Pythagorean theorem does not lead to a vicious circle. Therefore, we may assume the convergence of the geometric series

$\displaystyle 1+x+x^2+\ldots+=\frac{1}{1-x}.$

as a basis for a proof of the theorem.

John's starting point was the presence of similar right triangles formed by the altittude from the right angle:

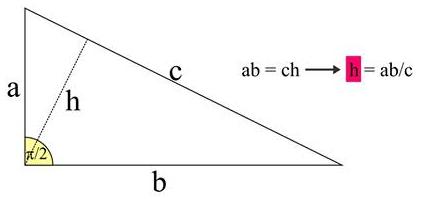
The triangles in gray in the figure below are all similar with the right triangle above, implying the proportions that follow the diagrams:

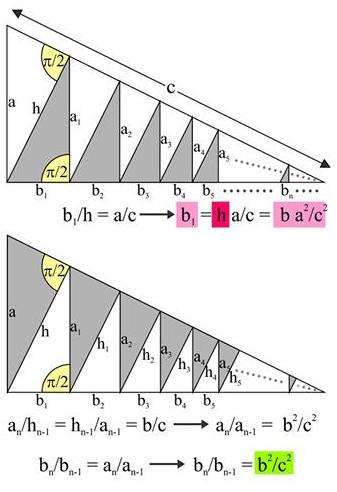
Without much ado,

$\displaystyle b=b_1+b_2+b_3+\ldots =b_1+\frac{b^2}{c^2}b_1+\frac{b^4}{c^4}b_1+\ldots$

where setting $\displaystyle x=\frac{b^2}{c^2}\lt 1$ and applying the summation formula for the geometric series leads to

$\displaystyle \begin{align} b=b_1+b_2+b_3+\ldots b&=b_1(1+x+x^2+\ldots)\\ &=b\frac{a^2}{c^2}\cdot\frac{1}{1-b^2/c^2}\\ &=b\frac{a^2}{c^2-b^2}, \end{align}$

from which $\displaystyle\frac{a^2}{c^2-b^2}=1.$

|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny