Pythagorean Theorem for the Reciprocals
Let $a,b$ be the legs of a right triangle, $h$ its altitude from the right angle:
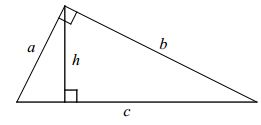
Then
$\displaystyle\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{h^2}.$
[Alsina and Nelsen, p.73] give a proof with no illustration. Let $c$ be the hypotenuse. Multiplying the sides of the triangle by $\displaystyle\frac{1}{ab}$ gives a triangle similar to the original one with sides $\displaystyle\frac{1}{b},$ $\displaystyle\frac{1}{a},$ and $\displaystyle\frac{c}{ab}.$ But $ab = 2S=ch,$ where $S$ is the area of the triangle, implying $\displaystyle\frac{1}{h}=\frac{c}{ab}.$ Thus the required identity is simply the Pythagorean theorem in the right triangle with sides $\displaystyle\frac{1}{a},$ $\displaystyle\frac{1}{b},$ and $\displaystyle\frac{1}{h}.$
As I already mentioned the illustration is missing from the book, but it does appear in Nelsen's earlier note:
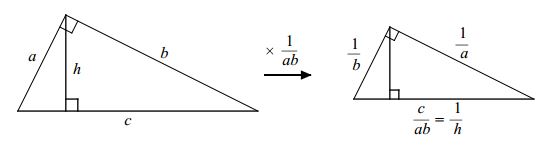
The diagram is self-explanatory. In the book, Alsina and Nelsen mention a proof of that identity by Vincent Ferlini. The proof comes with a diagram that on first inspection challenged my notion of proof without words. But the accompanying explanation that relied heavily on the diagram made the idea of the proof absolutely transparent. It's actually very straightforward.
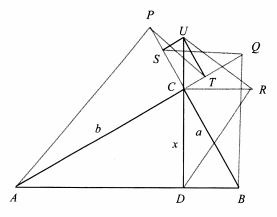
In the diagram, the right triangles $APT,$ $URD,$ and $SQB$ are constructed by making $CP,$ $CQ,$ and $CR$ all have length $1.$ Keep in mind that the square of the length of an altitude to the hypotenuse of a right triangle is the product of the lengths of the segments into which the altitude divides the hypotenuse. This shows that in $\Delta DRU,$ $CU$ has length $\displaystyle\frac{1}{x},$ in $\Delta APT,$ $CT$ has length $\displaystyle\frac{1}{b},$ and in $\Delta BQS,$ $CS$ has length $\displaystyle\frac{1}{a}$. The rectangle $CTUS$ then gives the upside-down Pythagorean theorem.
References
- C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010
- R. B. Nelsen, Proof Without Words: A Reciprocal Pythagorean Theorem, Mathematics Magazine, 82, n. 5, December 2009, p. 370
- V. Ferlini, Mathematics without (many) words, The College Mathematics Journal, 33, n. 2, March 2001, p. 170
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73587665
