Proof of Pythagoras' Theorem
The following is due to Dao Thanh Oai (Vietnam):
Let $CH_c$ and $BH_b$ be two altitudes in $\Delta ABC.$
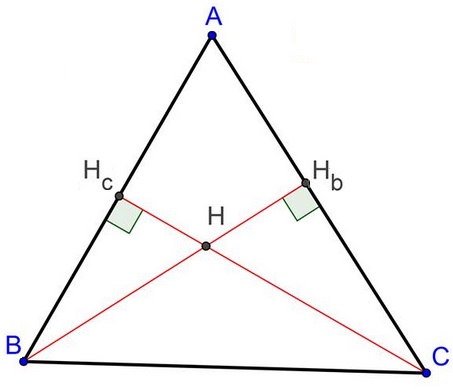
Then
$BC^{2}=AB\cdot BH_{c}+AC\cdot CH_{b}.$
Proof
Denoting angles at the vertices of the triangle $\alpha ,\beta ,\gamma$ we find several lengths as shown in the diagram below:
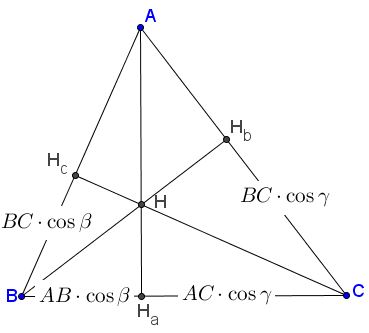
We, therefore, have:
$\begin{align} AB\cdot BH_{c}+AC\cdot CH_{b} &= AB\cdot BC\cdot\cos\beta + AC\cdot BC\cdot\cos\gamma\\ &=BC(AB\cdot\cos\beta+AC\cdot\cos\gamma)\\ &=BC\cdot(BH_a + CH_a)\\ &=BC\cdot BC = BC^{2}. \end{align}$
We could have done that without trigonometry but from similutude of triangles:
$\displaystyle\frac{BH_c}{BC}=\frac{BH_a}{AB}$ and $\displaystyle\frac{CH_b}{BC}=\frac{CH_a}{AC}$
It follows that
$\begin{align} AB\cdot BH_{c}+AC\cdot CH_{b} &= BC\cdot BH_a + BC\cdot CH_a\\ &=BC\cdot(BH_a + CH_a)\\ &=BC\cdot BC = BC^{2}. \end{align}$
The Pythagorean theorem is obtained when angle at $A$ is right.
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73794826