Modern Day Sangaku
In the configuration shown $OA\perp OB.$
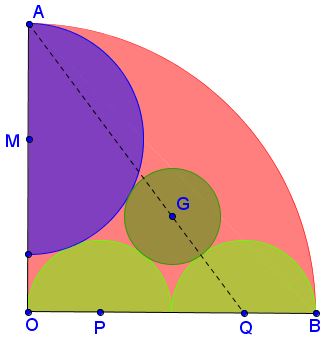
Prove that $A,$ $G,$ $Q$ are collinear.
Proof 1
Without loss of generality we may choose $(P):\,(x-1)^2+y^2=1,$ and $(Q): (x-3)^2+y^2=1$ (which means that $(O): x^2+y^2+4^2.)$ If $M=(0,a),$ $(M):\,x^2+(y-a)^2=(4-a)^2$ and, since $(P)$ and $(M)$ are externally tangent, $PM=1+4-a=5-a,$ so that $1+a^2=(5-a)^2,$ from which $a=\displaystyle\frac{12}{5}$ and $4-a=\displaystyle\frac{8}{5}.$
Now consider a generic circle $(C)$ centered at $C(2,b)$ and externally tangent to $(P)$ and $(Q).$ Due to the symmetry, $(C):\,(x-2)^2+(y-b)^2=r^2,$ with $r$ being the radius of $(C).$ To find $b$ assume, $A,$ $C,$ and $Q$ are collinear. We have
$\left| \begin{array} . 2 & b & 1\\ 0 & 4 & 1\\ 3 & 0 & 1\\ \end{array} \right|=0,$
implying $b=\displaystyle\frac{4}{3}.$
From $CP=r+1$ we get via the Pythagorean theorem $1^{2}+\displaystyle\frac{16}{9}=(r+1)^{2},$ implying $r=\displaystyle\frac{2}{3}.$ Now, for $(C)$ and $(M)$ to be externally tangent, we'll need $CM=\displaystyle\frac{8}{5}+{2}{3},$ which would lead to $\displaystyle 4+4\frac{64}{225}=4\frac{289}{225},$ which is obviously true. But there is a unique circle externally tangent to $(M),$ $(P),$ and $(Q).$ Hence $(C)=(G)$ which furnishes the proof.
Proof 2
Perhaps, more in the spirit of Edu period, here's an elementary solution that does not use much beyond the Pythagorean theorem. Assume $OM=4,$ such that $OP=1.$
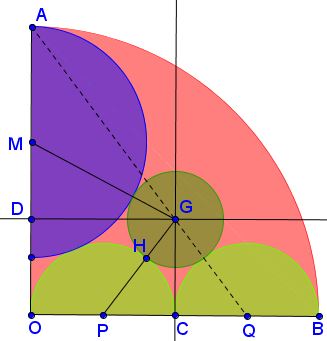
Let $C$ be the midpoint of $OB.$ In $\Delta MOP,$ $(4-R)^{2}+1^{2}=(R+1)^2,$ where $R$ is the radius of $(M).$ We find $R=1.6.$
Denote $x=CG$ and $r,$ the radius of $(G).$ In $\Delta DGM,$
$(2.4-x)^2+2^2=(1.6+r)^2.$
In $\Delta CGP,$
$x^2 +1^2=(r+1)^2.$
Combining the two equations, we get $r=6-4x$ which, if substituted into the second one, leads to the quadratic equation $15x^2-56x+48=0,$ with two roots $\displaystyle x=\frac{4}{3}$ and $\displaystyle x=\frac{12}{5},$ the latter is obviously too big. With $\displaystyle x=\frac{4}{3},$ $r=\displaystyle\frac{2}{3}.$
Now, triangles $QOA$ and $QCG$ are similar (since $\displaystyle\frac{OA}{OQ}=\frac{CG}{CQ}=\frac{4}{3}$ which shows that the points $A,$ $G,$ $Q$ are indeed collinear.
Extras
It is hard to miss the fact that $\Delta QOA$ is the famous $3-4-5$ triangle.
Additionally, the lower end $E$ of the diameter $AE$ of $(M)$ and point $H$ of the tangency of $(P)$ and $(G)$ lie on a line parallel to $OB:$ $EH\parallel OB.$
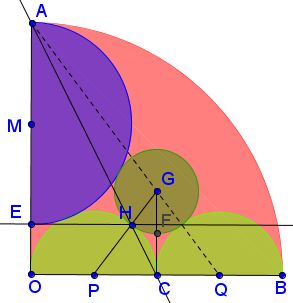
The lowest point $F$ of $(G)$ is midway from $G$ to $C$ on $OB.$
$H$ also lies on $AC.$
Acknowledgment
This problem by Ruben Dario has been posted by Leo Giugiuc at the CutTheKnotMath facebook page. The first solution is by the Romanian Crew.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73587144
