Planar Sets with Integer Distances between Points

Consider any Pythagorean triple $p^2+q^2=r^2$ and the angle $\alpha$ in the triangle formed by $p,q,r$ with $\displaystyle \cos\alpha=\frac{p}{r}$ and $\displaystyle \sin\alpha=\frac{q}{r},$ so that both sine and cosine of $\alpha$ are rational. We may also consider point $(\cos\alpha,\sin\alpha)$ on the unit circle or the corresponding complex number $s=e^{i\alpha}.$ Now consider the set

$S=\{e^{im\alpha}=(\cos\alpha+i\sin\alpha)^m:\,m=1,2,\ldots\}.$

Obviously, all points of set $S$ have rational coordinates. We'll show that the pairwise distances between two points from $S$ are also rational. Indeed,

$\displaystyle \begin{align} |e^{im\alpha}-e^{in\alpha}|&=\sqrt{(\cos m\alpha-\cos n\alpha)^2+(\sin m\alpha-\sin n\alpha)^2}\\ &=\sqrt{2-2\cos 2(m-n)\alpha}=\sqrt{4-4\cos^2(m-n)\alpha}\\ &=2|\sin (m-n)\alpha|. \end{align}$

Since $e^{i(m-n)\alpha}\in S,$ we know that $2|\sin (m-n)\alpha|$ is a rational number. As the set $S$ is finite, we may expand the unit circle by the LCM of the denominators of its points thus getting a set on a big circle, with the pairwise distances between its points all integer.

Assume there is set $S\subset\mathbb{R}^2$ with not all points collinear. Then there are three points $A,B,C\in S$ that from a non-degenerate $\Delta ABC.$ Note that the side lengths, $a,b,c,$ of $\Delta ABC$ are integer.

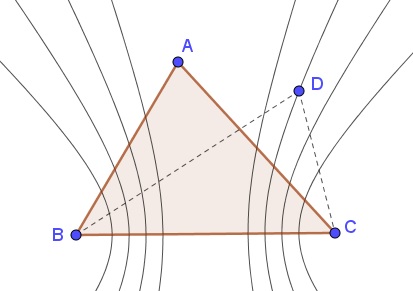
Let $D\in S,$ different from $A,B,C$ but the distances from $D$ to all three are integer. Thus, for example, $|BD-BC|$ is also integer. However, observe that, by the triangle inequality, $|BD-BC|\lt BC=a,$ meaning that $|BD-BC|$ may only take a finite number of values, viz., $0, 1, 2, \ldots, a-1.$ In other words, $D$ may only lie on a final set of hyperbolas with foci at $B$ and $C.$ The same naturally holds for hyperbolas with foci at $A$ and $B$ or $A$ and $C.$

Any two hyperbolas intersect at at most four points, implying that the aforementioned sets of hyperbolas have a finite set of common points, their intersections. Thus $D$ necessarily is bound to belong to a finite set of points, making $S$ also finite.

Ross Honsberger, Mathematical Gems, The Two-Year College Mathematics Journal, Vol. 10, No. 5 (Nov., 1979), pp. 344-347. In particular, Honsberger credits the solution for part 2 to Paul Ërdos.