Problem 5 from the IMO 2004

Here is Problem 5 from the IMO 2004:

In a convex quadrilateral ABCD the diagonal BD does not bisect the angles ABC and CDA. The point P lies inside ABCD and satisfies ∠PBC = ∠DBA and ∠PDC = ∠BDA. Prove that ABCD is a cyclic quadrilateral if and only if AP = CP.

The solution below is by Vo Duc Dien who dedicated it to his former teacher Le Chi De.

The condition AP = CP is necessary. Indeed, assume point B is already on the circumcircle of ΔACD.

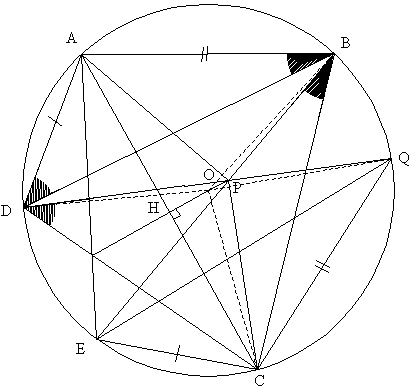
problem #5 from 2004 IMO

Extend DP to intercept the circle at Q and BP to intercept the circle at E. Consider two quadrilaterals ABPD and CQPE. Since ∠ABD = ∠EBC we get AD = EC. Further

∠ABE = ∠DBC = ∠DQC
∠DPB = ∠EPQ
∠ADQ = ∠BDC = ∠BEC.

Therefore ∠ DAB = ∠ECQ, for the sum of the angles of a quadrilateral is 360°.

Two triangles DAB and ECQ are identical since ∠DAB = ∠ECQ, AD = EC and AB = CQ; this implies DB = EQ.

It follows that triangles DPB and EPQ are also identical (two angles on each side of DB and EQ are equal which gives us PB = PQ.

Therefore triangles ABP and CQP are identical since AB = CQ, PB = PQ and the two angles ABP and CQP are equal which implies AP = PC.

The condition AP = PC is sufficient. Indeed, assume AP = PC and prove ABCD is a cyclic quadrilateral:

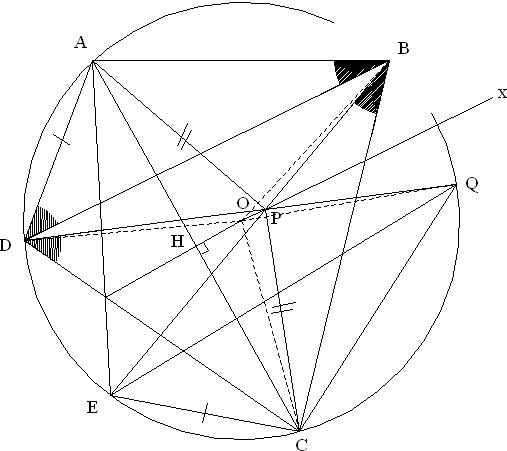
problem #5 from 2004 IMO

Consider the circumcircle of ΔADC. From C draw a line that intercepts the circle at E and that CE = AD.

Choose arbitrary point P and draw a line to connect E and P and extend it to cut the circle at B to satisfy the first condition ∠ABD = ∠PBC since CE = AD.

Now let O be the circumcenter of ΔABC. We note that OP is the axis of symmetry of AD and CE. Extend DP to intercept the circle at Q.

Let's show that the assumption AP ≠ PC leads to a contradiction. If AP ≠ PC then CQ ≠ AB since Ox (extension of OP) is the line of symmetry. Since Q is on the circle and AB ≠ CQ, ∠ADB ≠ ∠PDC, implying that B is not symmetrical to Q in Ox. Therefore B is not on the circle.

So P has to be on Ox for B to be on the circle so that AP = PC implies that ABCD is a cyclic quadrilateral.

71924450