Generalized Carnot's theorem
Carnot's theorem is a direct application of the theorem of Pythagoras. It's a nice little theorem that is unlikely to be rediscovered with dynamic geometry software. However, Miguel Ochoa Sanchez (Peru) has come up with an interesting generalization.
Miguel Ochoa Sanchez
19 December 2015
Point $O$ is within $\Delta ABC.\;$ Let points $D,$ $E,$ and $F$ be located on the sides $BC,$ $AC,$ and, respectively, $AB$ of the triangle such that the three angles $AEO,$ $BFO,$ and $CDO$ are all equal to, say, $\phi.$
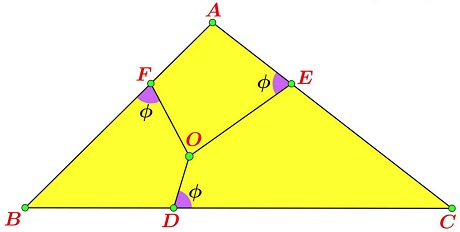
Then
$AF^{2} - BF^{2} + BD^{2} - CD^{2} + CE^{2} - AE^{2} = 4[\Delta ABC]\cdot\cot\phi,$
where $[\Delta ABC]$ is the area of $\Delta ABC].$
The proof depends on the following
Lemma
Let $D$ be on the side of $BC$ of $\Delta ABC;$ $\angle ADC=\phi.$
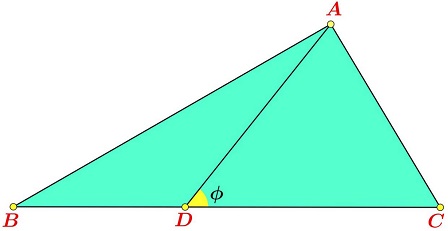
Then
$CD^{2} - BD^{2} = AC^{2} - AB^{2} + 4[\Delta ABC]\cdot\cot\phi,$
Proof of Lemma
Drop the perpendicular $AH$ to $BC.$
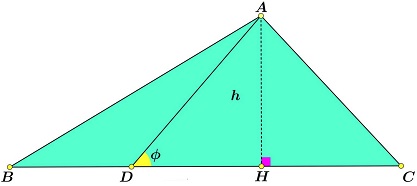
Then $DH=AH\cdot\cot\phi,$ $CH=CD-AH\cdot\cot\phi.$ By the Pythagorean theorem,
$\begin{align} AC^{2}-AB^{2}&=CH^{2}-BH^{2}\\ &=(CD-AH\cdot\cot\phi)^{2}-(BD+AH\cdot\cot\phi)^{2}\\ &=CD^{2}-BD^{2}-2\cdot CD\cdot AH\cdot\cot\phi-2\cdot BD\cdot AH\cdot\cot\phi\\ &=CD^{2}-BD^{2}-2\cdot BC\cdot AH\cdot\cot\phi\\ &=CD^{2}-BD^{2}-4\cdot[\Delta AB]\cdot\cot\phi. \end{align}$
Proof of Theorem
We'll use the notations as in the diagram below:
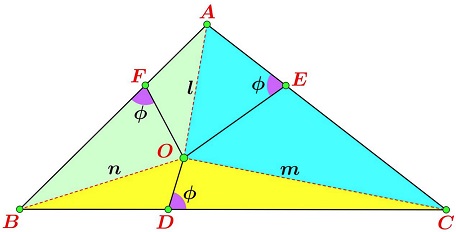
Apply the lemma to triangles $BOC,$ $AOB,$ $AOC$ to obtain
$\begin{align} CD^{2}-BD^{2}&=m^{2}-n^{2}+4[\Delta BOC]\cot\phi\\ BF^{2}-AF^{2}&=n^{2}-l^{2}+4[\Delta BOC]\cot\phi\\ AE^{2}-CE^{2}&=l^{2}-m^{2}+4[\Delta BOC]\cot\phi. \end{align}$
Add the three up:
$\begin{align} CD^{2}-BD^{2}&+BF^{2}-AF^{2}+AE^{2}-CE^{2}\\ &=4[\Delta BOC]\cot\phi+4[\Delta BOC]\cot\phi+4[\Delta BOC]\cot\phi\\ &=4[\Delta ABC]\cot\phi. \end{align}$
There is a natural generalization to the case of an $n\text{-gon},$ with $n\ge 3:$
With $P_{n+1}=P_1,$
$\displaystyle\sum_{k=1}^{n}P_iQ_i^2-\sum_{k=1}^{n}Q_iP_{i+1}^2=4[P_1P_2\ldots P_n]\cot\phi.$
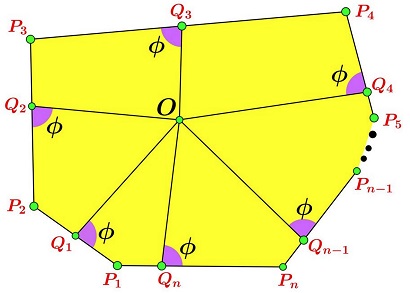
The proof is analoguous to the case where $n=3.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573851
