Construction: Parallel Line through Point

1. Choose a point $A\,$ on $\ell\,$ and draw circle $A(P)\,$ with center $A\,$ throught $P.$

2. Choose another point $B\,$ on $\ell\,$ and draw circle $B(P)\,$ with center $B\,$ throught $P.$

   Mark point $C\,$ - the second intersection of the two circles.

3. Draw line $CA\,$ and let $D\,$ be the second intersection of that line with circle $A(P).$

   

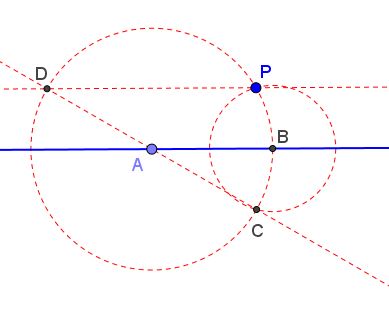
4. Line $PD\,$ is parallel to $\ell.$

Due to symmetry, $PC\perp\ell,\,$ whereas $CD\,$ is a diameter of $A(P).\,$ It follows $\angle CPD = 9^{\circ},\,$ hence, $PD\parallel\ell.$

The construction has been communicated to me by Dr. Ted Courant, Mathematics Department, New Roads School.