Pythagoras, from the Power of a Point - Again

Several times previously (proofs 22, 43, 71) the Pythagorean theorem has been derived from the Power of a Point theorem. Below is another example of the power of that theorem devised by Bùi Quang Tuån. Bùi's approach is illustrated by the following diagram

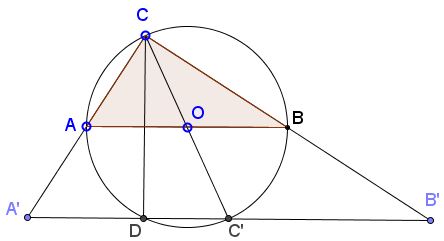
proof 105 of the Pythagorean theorem

Let $ABC$ be a right triangle $(\angle ACB=90^{\circ}),$ with the sides $a=BC,\,b=AC,\,c=AB,$ as usual. We are to prove that $a^{2}+b^{2}=c^{2}.$

Let $A'$ be the reflection of $C$ in $A,$ $B'$ in $B,$ $C'$ in $O$ the circumcenter of $\Delta ABC$ (the midpoint of $AB).$ The three points $A',\,B'\,C'$ are obtained by a homothety with center $C$ and coefficient $2$ from $A,\,O,\,B$ and, therefore, are collinear. Line $A'B'$ meets the circumcircle $(ABC)$ in $C'$ and the second time in $D.$

Note that $A'C=2b,\,B'C=2a,\,A'B'=2c,$ whereas $A'C'=B'C'=c.$ Assuming, as depicted in the diagram, that $a\gt b,$ we have by the Power of a Point theorem,

$A'A\cdot A'C=A'D\cdot A'C',$ i.e., $2a^{2}=(c-DC')\cdot c,$
$B'B\cdot B'C=B'D\cdot B'C',$ i.e., $2b^{2}=(c+DC')\cdot c.$

Adding the two gives $2a^{2}+2b^{2}=2c^{2}$ - one step away from the Pythagorean theorem.

71921399