A Matter of Collinearity:
Metamorphosis of a Problem
Dao Thanh Oai (Vietnam) has posted the following problem at the CutTheKnotMath facebook page:
In $\Delta ABC,$ $D,$ $E,$ $F$ lie on $BC,$ $CA,$ $AB,$ respectively. $AFA'E,$ $BFB'D,$ $CEC'D$ are three parallelograms.
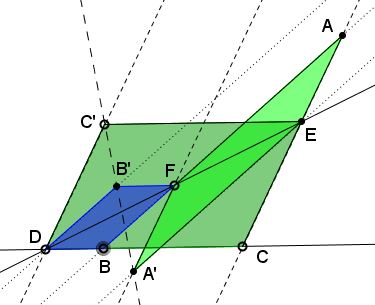
Show that $A',$ $B',$ $C'$ are collinear.
In an attempt to develop a dynamic illustration, it occurred to me that the problem may be more naturally put in a little different, more symmetric (concerning the constituent objects) frame:
Given three parallelograms $CEC'D,$ $BFB'D,$ $AFA'E$ such that $A\in CE,$ $B\in CD,$ $F=DE\cap AB.$ Prove that $A',$ $B',$ $C'$ are collinear.
Spending more time pondering this problem over, I develop a feeling that symmetry is still lacking. As a result I came up with a different formulation:
Given three sets of three parallel lines each through three collinear points $D,$ $E,$ $F:$ $DC'\parallel FA'\parallel CEA,$ $EC'\parallel FB'\parallel BCD,$ $DB'\parallel BEA\parallel EA'.$
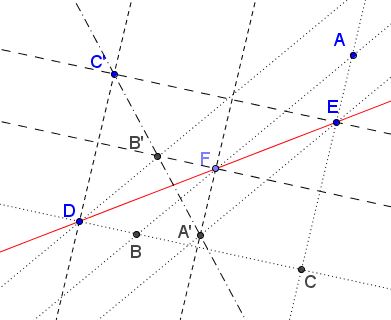
Prove that points $A',$ $B',$ $C'$ are collinear.
This formulation did not seem to make the problem more symmetric, but it appeared to suggest that the original points $A,$ $B,$ $C$ played no essential role within the problem. Removing the points made it clear that a couple of lines had also been redundant and led to the next formulation:
Given three collinear points $D,$ $E,$ and $F$ and three pairs of parallel lines: $DC'\parallel FA',$ $EC'\parallel FB',$ $DB'\parallel EA'.$
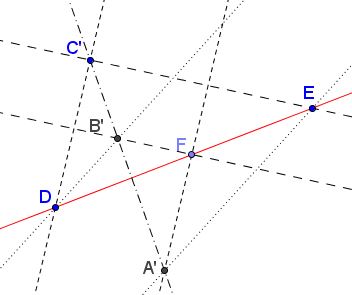
Prove that points $A',$ $B',$ $C'$ are collinear.
Now the formulation became quite symmetric: there are three collinear points and three pairs of parallel lines, with two lines (from different pairs) passing through each of the three points. The lines through the points can be recombined to form three collinear intersections.
Symmetry has a virtue of clarifying the picture: the problem illustrates a property of three sets of parallel lines and, as such, is of affine character. If so, it may be useful to select a configuration that affords an easy treatment. It also seems that at this point changing notations mady lead to additional simplification:
In Cartesian (or affine) coordinates, points $A(0,b),$ $B(a,0),$ and $C(\alpha ,\beta )$ are collinear. $AD\parallel BE$ where $D$ is on $y=\beta$ and $E$ on $x=\alpha.$
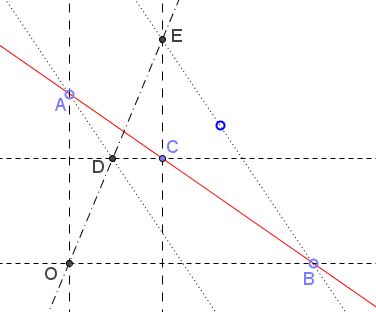
If $O$ is the origin, prove that $O,$ $D,$ $E$ are collinear.
Proof
Let $m$ be the slope of the two parallel lines, $AD$ and $BE.$ Then the equation of the first is $y=mx+b,$ that of the second $y=m(x-a).$ The fact that the points $A,$ $B,$ $C$ are collinear is expressed as
$\alpha b+\beta a=ab.$
We may easily find the coordinates of points $D$ and $E:$ $\displaystyle D=(\frac{\beta - b}{m},\beta )$ and $E=(\alpha ,m(\alpha -a)).$ The slopes of the lines $OD$ and $OE$ are, respectively, $\displaystyle\frac{\beta m}{\beta -b}$ and $\displaystyle\frac{m(\alpha -a)}{\alpha}.$ The two are equal iff
$\alpha\beta m= m(\alpha -a)(\beta -b),$
which is equivalent to the condition $\alpha b+\beta a=ab$ of collinearity of $A,$ $B,$ and $C.$
Another solution
This applies to the penultimate reformulation:
Given three collinear points $D,$ $E,$ and $F$ and three pairs of parallel lines: $DC'\parallel FA',$ $EC'\parallel FB',$ $DB'\parallel EA'.$

Prove that points $A',$ $B',$ $C'$ are collinear.
Machó Bónis has observed that the problem is a particular case of Papus' theorem, with one triple of points (each defined by a pair of parallel lines) lying on a line at infinity. This indeed may have been noticed at the outset, making the matter of parallelogram a red herring. I missed that.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580908
