An Identity for Regular Tetrahedra
Here's a problem posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page:
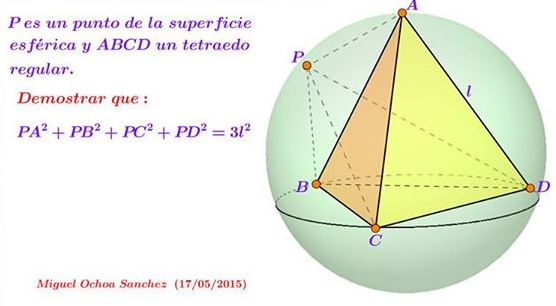
Even though the beautiful picture requires no explanation, I put my interpretation in words - if only out of habit:
$P$ is a point on the circumsphere of the regular tetrahedron $ABC$ of edge length $l.$ Then
$PA^{2}+PB^{2}+PC^{2}+PD^{2}=3l^{2}.$
The proof by Leo Giugiuc makes use of the spherical coordinates. Assume for simplicity and without loss of generality $l=4\sqrt{3},$ we can choose $A=(0,0,4\sqrt{2}),\;B=(4,0,0),\;C=(-2,2\sqrt{3},0),\;D=(-2,-2\sqrt{3},0)$ such that the circumcenter $O=(0,0,\sqrt{2})$ and the circumradius $R=3\sqrt{2}.$ Finally, we assume $P$ is an arbitrary point on the sphere $S(O,R),$ with coordinates
$P=(3\sqrt{2}\cos t, 3\sqrt{2}\sin t\cos u, \sqrt{2}+3\sqrt{2}\sin t\sin u).$
So we have
$\begin{align} PA^{2}&=18\cos^{2}t+18\,\sin^{2}t\,\cos^{2}u+18(1-\sin t\,\sin u)^{2}\\ PB^{2}&=(4-3\sqrt{2}\cos t)^{2}+18\,\sin^{2}t\,\cos^{2}u+2(1+3\sin t\,\sin u)^{2}\\ PC^{2}&=(2+3\sqrt{2}\cos t)^{2}+(2\sqrt{3}-3\sqrt{2}\sin t\,\cos u)^{2}+2(1+3\sin t\,\sin u)^{2}\\ PD^{2}&=(2+3\sqrt{2}\cos t)^{2}+(2\sqrt{3}+3\sqrt{2}\sin t\,\cos u)^{2}+2(1+3\sin t\,\sin u)^{2}\\ \end{align}$
The easiest way to proceed is to notice that in the sum of the four equalities, the term $(\sin t,\sin u)^{2}$ comes with the coefficient of $72$ - the same as the term $(\sin t\,\cos u)^{2}.$ Thus these two add up to $72\sin^{2}t.$ Luckily, the term $\cos^{2}t$ also comes with the coefficient $72$ so that this is the sum of those two. The mixed term $\sin t\,\cos u$ has a coefficient of $0$ and the free coefficients add up to $144=3(4\sqrt{3})^{2}.$
It may be worth mentioning (and is easily verified) that, for a point $P$ on the circumcircle of an equilateral $\Delta ABC,$ with side length l$, a similar identity holds:
$PA^{2}+PB^{2}+PC^{2}=2l^{2}.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575081
