Assigning Numbers to Points in the Plane

Here is Problem 6 from the 2001 USAMO:

Each point in the plane is assigned a real number such that, for any triangle, the number at the center of its inscribed circle is equal to the arithmetic mean of the three numbers at its vertices. Prove that all points in the plane are assigned the same number.

Solution

Solution

The solution is by Michael Hamburg, St. Joseph's HS, South Band, Indiana, for which he was awarded The Clay Olympiad Scholar Award from the Clay Mathematics Institute. The judges observed that only 9 out of 260 participants solved the problem correctly. They praised Michael's ingenuity and elegance noting that the simple diagram practically amounts to a proof without words.

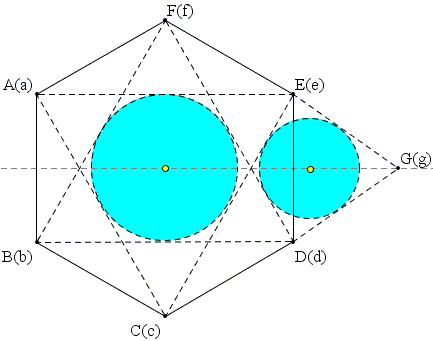
2001 USAMO, problem 6

Let A and B be two arbitrary points. Form a regular hexagon ABCDEF and let G be the intersection of CD and EF. Note that points A, F, E are the reflections of points B, C, D in the line through G parallel to both AE and BD. It follows that the triangles ACE and BDF share the incircle and hence the incenter. The same holds for triangles CEG and DFG. Denoting the number assigned to a point by the corresponding lower case letter, we have two equations:

a + c + e = b + d + f and
d + f + g = c + e + g.

Adding the two and simplifying yields a = b; and we are done.

If we replace in the formulation of the problem the "inscribed" with "circumscribed" the statement holds and here is a

Solution

We first show that, for any circle, the numbers assigned to its points are all the same.

So pick circle C(O), with center O. Choose three points P, Q, X on C(O).

p + q + x = 3o.

Fix, C(O), P, and Q, and let X change over C(O). Clearly, x = 3o - (p + q) does not depend on a specific position of X on C(O). Fixing X and Q, and then also X and P, we see that p and q take up the same common value, which proves that the number assignment is constant on any circle.

Any two points lie on a multitude of circles; but just one will suffice. Since on any circle the number assignment is constant, the numbers assigned to the given two points are equal.

Remark

It may be observed that the fact that the assigned numbers were real played no role in the solution. Any set of numbers that is closed under the operation of taking the average of any three of them would do as well. In particular, the numbers in the problem could be rational, imaginary, infinitesimal, hyperreal or even surreal or quaternion. Naturally, vectors and matrices could be used as well. To use whole numbers we'd need to replace the "average" with the "sum". If 0 is excluded, the "product" could be used with the same degree of success.

References

C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, pp. 47-48

41173458