Sylvester's Problem, Gallai's Solution

The Sylvester Problem has been posed by James Joseph Sylvester in 1893 in Educational Times:

Let $n$ given points have the property that the line joining any two of them passes through a third point of the set. Must the $n$ points all lie on one line?

T. Gallai's proof has been outlined by P. Erdös in his submission of the problem to The American Mathematical Monthly in 1943.

Solution

Given the set $\Pi$ of noncollinear points, consider the set of lines $\Sigma$ that pass through at least two points of $\Pi.$ Such lines are said to be connecting. Among the connecting lines, those that pass through exactly two points of $\Pi$ are called ordinary.

Choose any point $p_{1}\in\Pi.$ If $p_{1}$ lies on an ordinary line we are done, so we may assume that $p_{1}$ lies on no ordinary line. Project $p_{1}$ to infinity and consider the set of connecting lines containing $p_{1}.$ These lines are all parallel to each other, and each contains $p_{1}$ and at least two other points of $\Pi.$ Any connecting line not through $p_{1}$ forms an angle with the parallel lines; let $s$ be a connecting line (not through $p_{1})$ which forms the smallest such angle:

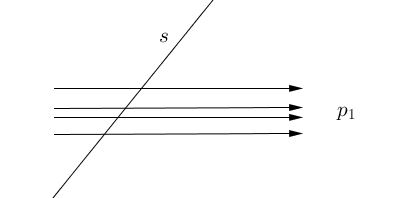
Gallai's proof of Sylvester's problem, part 1

Then $s$ must be ordinary! For suppose $s$ were to contain three (or more) points of $\Pi,$ say, $p_{2},$ $p_{3},$ $p_{4}$ named so that $p_{3}$ is between $p_{2}$ and $p_{4}:$

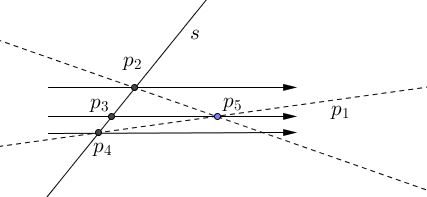
Gallai's proof of Sylvester's problem, part 2

The connecting line through $p_{3}$ and $p_{1}$ (being not ordinary) would contain a third point of $\Pi,$ say $p_{5},$ and now either the line $p_{2}p_{5}$ or the line $p_{4}p_{5}$ would form a smaller angle with the parallel lines than does $s.$

References

P. Borwein, W. O. J. Moser, A survey of Sylvester's problem and its generalizations, Aequationes Mathematicae 40 (1990) 111 - 135
P. Erdös, R. Steinberg, Problem 4065 [1943, 65], The American Mathematical Monthly, Vol. 51, No. 3 (Mar., 1944), pp. 169-171
J. J. Sylvester, Educational Times, Mathematical Question 11851, vol. 59 (1893), p. 98

71925115