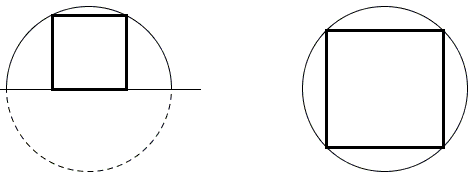
Squares in Semicircle and Circle

Prove the following statement

A square inscribed in a semicircle has 2/5 the area of a square inscribed in a circle of the same radius.

squares inscribed into a semicircle and a circle of the same radius - problem

Proof

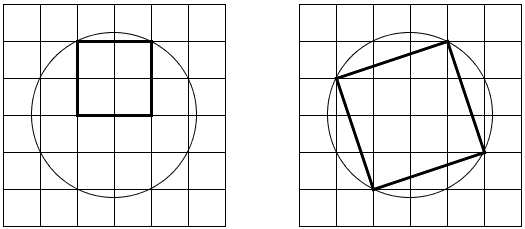
squares inscribed into a semicircle and a circle of the same radius - solution

Taking the common radius of the circles to be √5, draw the circles centered in a node of a unit square grid as shown. On the right, the side of the square is a hypotenuse of a right triangle with legs 1 and 3 and therefore has a side length of √10 and the area of 10.

On the left the square has area of 4. The ratio of the two areas is therefore 4/10 = 2/5, as required.

References

C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, p. 123

72189876