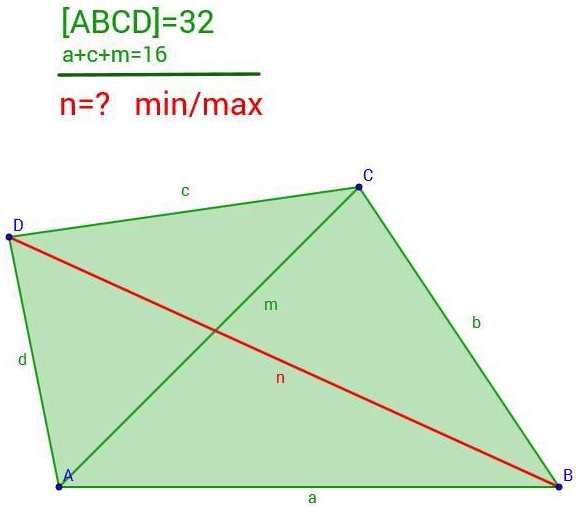
Extremal Problem in a Quadrilateral

The following problem has been posted by Leo Giugiuc at the CutTheKnotMath facebook page; Leo borrowed it from the Olimpiada pe Scoala (The School Yard Olympiad) facebook group. It appears that the problem, submitted by the Socialist Republic of Czechoslovakia, has been in the short list of the first IMO (1959). The solution below is by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.

Extremal problem in a quadrilateral

Solution

Observe that

$64=ma\sin\angle BAC+mc\sin\angle ACD\le ma+mc=m(a+c)=m(16-m).$

But, by the AM-GM inequality, $\displaystyle m(16-m)\le\left(\frac{m+(16-m)}{2}\right)^2=64.$ So it follows that $m(16-m)=64,$ implying the unique value, $m=8.$ As a side effect, $\sin\angle BAC=\sin\angle ACD=1,$ such that both angles equal $90^{\circ},$ making $ABCD$ a trapezoid: $AB\parallel CD.$

Let $E$ be the intersection of the diagonals. Then triangles $ABE$ and $CED$ are similar, $c=8-a,$ $CE=8-AE$ and $\displaystyle\frac{a}{8-a}=\frac{AE}{8-AE},$ so that $AE=a,$ for, function $\displaystyle f(x)=\frac{x}{8-x}$ is 1-1 on $(0,8).$ Thus, we have $BE=a\sqrt{2}$ and, by analogy, $DE=c\sqrt{2}.$ Finally, $n=8\sqrt{2}$ - the only value tat satisfies the constraints.

71950068