Gauss and Euler Integrals
The function $f(x)=e^{-x^2}$ whose graph is an immediately recognizable bell-curve
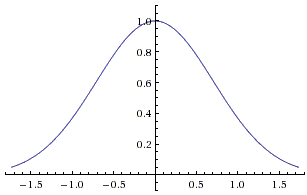
plays a fundamental role in probability and statistics. The so-called normal distribution:
is defined via normalization of the integral
Below, we are going to establish this identity. An ingenious trick works like magic. (The integral falls into the category of dauntingly looking integrals that can be computed easily if one knows how.)
The whole exercise of squaring the integral was to obtain $x^{2}+y^2$, for $x^{2}+y^{2}=r^2$ is easily handled in polar coordinates $(r, \theta)$, $0\le r\lt\infty$, $0\le\theta\lt 2\pi$. With the substitution $x = r\text{cos}(\theta)$ and $y = r\text{sin}(\theta)$, $dxdy=r dr d\theta$. So we have
implying
The integral $I$ is known as the Gaussian integral (and the normal distribution as the Gaussian distribution). A substitution $x=\sqrt{t}$ leads to what is known as the Euler integral. The substitution applies to $I/2=\int_{0}^{\infty}e^{-x^2}dx$:
where $\Gamma$ is the famous $\Gamma$-function, popularly known due to its extension of the factorials: for integer $n$, $\Gamma(n+1)=n!$ One may be excused for using the factorial symbol for fractional arguments, e.g., as the Euler integral shows $(-\frac{1}{2})!=\sqrt\pi$. From this we conclude that
References
- M. Erickson, Beautiful Mathematics, MAA, 2011
![]()
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73574619
