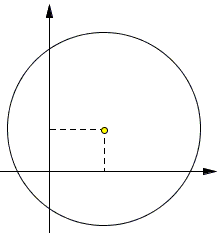
The point P = P(a, b) is located in the first quadrant. Consider a circle centered at the point P with radius greater than √a² + b², and denote the area of the part of this circle located in the i-th quadrant (i = 1, 2, 3, 4) by Si . Find S1 - S2 + S3 - S4.
The point P = P(a, b) is located in the first quadrant. Consider a circle centered at the point P with radius greater than √a² + b², and denote the area of the part of this circle located in the i-th quadrant (i = 1, 2, 3, 4) by Si . Find S1 - S2 + S3 - S4.
Solution
Draw two extra lines, x = 2a and y = 2b:
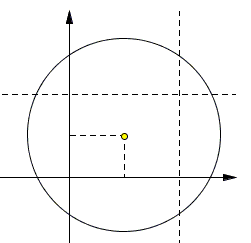
These two lines together with the two axes, split the area of the circle into 9 parts, eight of which cancel out in S1 - S2 + S3 - S4. The only remaining one is the central rectangle whose area is 2a·2b = 4ab.
|Contact|
|Front page|
|Contents|
|Up|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
