Is it possible to move the counters from the left half of the board to the right? The only allowed move is to jump over an adjacent (vertically, horizontally, or diagonally) counter. (The jumped over counters are not removed.)
The applet above helps you experiment with the problem. Click on the counter you wish to move and then click on the empty space where you want to place the counter.
Solution
The task is impossible for an N×(N + 1) board with N odd as becomes clear from the following diagram
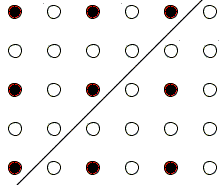
The counters originally located on the black spots will always stay on the black spots. The problem is there are six of them on the left and only three on the right.
Observe that removing up front one or two counters on the left still would not allow one to move the remaining ones to the right.
What happens when N is even? The task is still impossible, but for a slightly different reason. Introduce a system of coordinates (i, j) with the origin at the top left checker and extending leftward and downward. Associate with each checker the sum of the coordinates modulo 2, say, S(i, j) = i + j (mod 2). This is equivalent to coloring the spots again in two colors but now in the manner of a real checkerboard - interwining black and white spots. Checkers never change the color of the spots they are on.
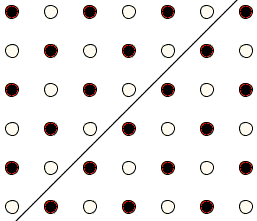
But clearly the number of, say, black spots in the left part of the board is different from their number on the right.
Reference
- M. Gardner, The Colossal Book of Short Puzzles and Problems, W. W. Norton, 2006, #10.12
|Contact|
|Front page|
|Contents|
|Up|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
