Color an N×N Board: No Colored Cell Touch

What is the largest number of cells of a 6×6 board that could be colored such that no two colored cells touch (not even at a corner)?

Solution


|Contact| |Front page| |Contents| |Up|

Copyright © 1996-2018 Alexander Bogomolny

What is the largest number of cells of a 6×6 board that could be colored such that no two colored cells touch (not even at a corner)?

An answer to the problem is 9 cells as shown in the left diagram below.

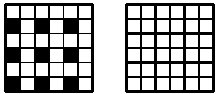
Why there could not be more colored cells? Because, as shown in the right diagram above, the board could be cut into 2×2 squares, and 9 is the number of such squares. It needs to be observed that no 2×2 square may contain more than 1 colored cell.

To generalize: in a (2N)×:(2N) one can color at most N² cells so that no two colored cells touch. For a (2N + 1)×(2N + 1) board, the number is (N + 1)².


Related material
Read more...

  • Sum of Integers
  • More than half of the integers from {1, 2, ..., 2n}
  • Consequences of Getting More Than a Half
  • Intersecting Subsets
  • Over-The-Counter Pigeonhole
  • Women in a theatre: Pigeonhole Principle
  • Pigeonhole Among Friends
  • Not Exceeding 24

    • |Contact| |Front page| |Contents| |Up|

    Copyright © 1996-2018 Alexander Bogomolny

    71537252