7 Points in a Triangle
Prove that among any seven points inside or on the boundary of a triangle of area 1, there are three points that form a triangle of area not exceeding 1/4.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander BogomolnyProve that among any seven points inside or on the boundary of a triangle of area 1, there are three points that form a triangle of area not exceeding 1/4.
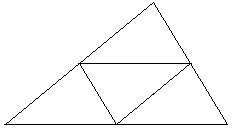
The areas (1 and 1/4) could lead to an attempt to divide the given triangle into 4, but then we would need 9 points to insure that at least three fall inside one of the smaller triangles:
Prove that among any nine points inside or on the boundary of a triangle of area 1, there are three points that form a triangle of area not exceeding 1/4.
What we are supposed to do when only seven points are given? We remove one midline:
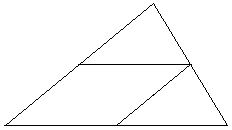
We have now a three way split of the given triangle. By the Pigeonhole principle,
This is done in several simple steps. So, there is a triangle in a parallelogram. Unless, its vertices lie on the boundary of the parallelogram, it can be expanded (with increase in the area) until they all do. This can be accomplished one vertex at a time by extending one of the sides to which it is incident.
Next, we'll move the vertices of the triangle to the vertices of the parallelogram. If all the vertices of the triangle are inside the sides of the parallelogram, then, by the Pigeonhole principle, some two of them lie on a pair of parallel sides. Keeping the side (of the triangle) the form parallel to itself the vertices of the triangle can slide along the sides of the parallelogram away from the third vertices until at least one of them falls onto a vertex of the parallelogram. Call this A.
At this point 1 or 2 vertices of the triangle may still lie in the interiors of the sides of the parallelogram. There are two cases to consider:
- One of these is on the side of the parallelogram incident to A. In this case, it can be moved away from A to another vertex of the parallelogram.
- Otherwise, draw through one of these a line parallel to the opposite side of the triangle. Part of the line will lie inside the parallelogram and cross it on some other side. Slide the vertex of the triangle along this line. The area of the triangle will not change.
Repeat the above steps if necessary. Eventually, the triangle will have two of its vertices at the adjacent vertices of the parallelogram and the third one on the opposite side, with the area 1/2 that of the parallelogram.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73581295
