Tying Knots In Brazil
Problem
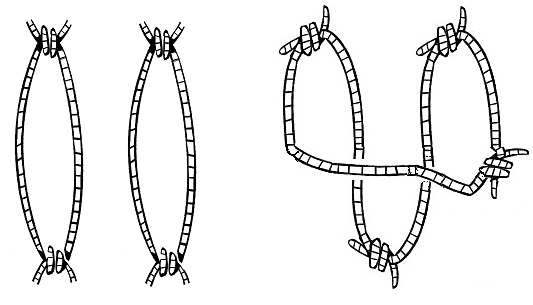
$\mathcal{A}$ is clutching three identical pieces of string in her fist, as illustrated below left.
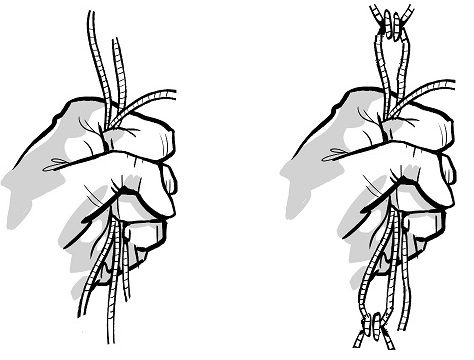
She asks $\mathcal{B}$ to tie two ends of the string, chosen at random, at either side of her fist, as illustrated above right, so that there is one free end at either side. The result could be as shown below:
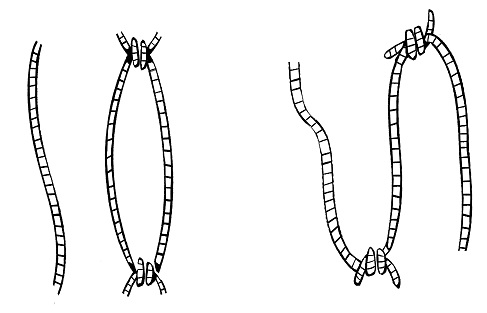
What is the probability that all the pieces are joined in one long piece? Same question for four or five strings, or even more.
Solution for three strings
There are three ways to tie the lose ends below the fist: $a\leftrightarrow b,$ $a\leftrightarrow c,$ $b\leftrightarrow c.$
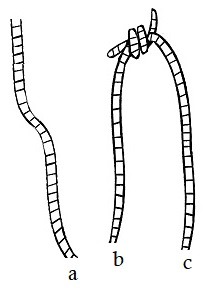
Two of them $(a\leftrightarrow b,$ $a\leftrightarrow c)$ lead to one long string so that the probability of that event is $\displaystyle \frac{2}{3}.$
Solution for four strings
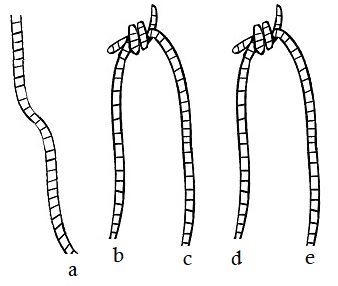
Given four string ends, when one knot is tied, the remaining two ends are left to be automatically tied. There is no choice.
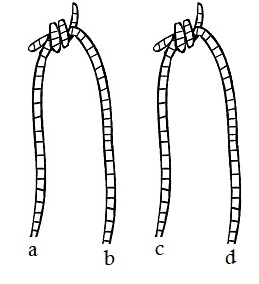
There are $\displaystyle {6\choose 2}=6$ ways to chose $2$ strings out of $2$ but there's doubling of the count as any two pairs of strings are counted twice. So all in all, there are just $3$ distinct ways to ties the lower ends: $a\leftrightarrow b\,+\,c\leftrightarrow d,$ $a\leftrightarrow c\,+\,b\leftrightarrow d,$ $a\leftrightarrow d\,+\,b\leftrightarrow c.$
On of these creates to small rings with two knots each, whereas two yield a single ring with four knots. Thus the probability of getting a long ring is $\displaystyle \frac{2}{3}.$
Solution for five strings
Tying two knots above the fist leaves us with the following configuration:
There are $\displaystyle \frac{1}{2}{5\choose 2}{3\choose 2}=15$ ways to form two distinct pairs of knots. To obtain one long string, the and $a$ needs to be tied. There are $4$ ways to accomplish that. Joining it with either $b,$ $c,$ $d,$ or $e$ will leave one end loose. Say, if $a$ is tied to $b,$ $c$ needs to be tied next. There are $2$ ways to accomplish that. Thus, in all, there are $4\cdot 2=8$ to tie two knots so as to form one long string. Thus, the probability of this happening equals $\displaystyle \frac{8}{15}.$
Acknowledgment
This is a puzzle by Alex Bellos from "The Guardian". Alex also devoted a tweet to introduce the puzzle (and this is how I learned about it.) Alex mentions that the problem was offered to 15-18 year olds at a Brazilian school olympiad in June, 2017.
My son Eli produced the graphics based on the original art that appeared in The Guardian. Any imperfections are due to my inept copy&paste that was occasionally needed.
![]()
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73579548
