Metamorphosis of a Quadratic Function
Problem

Solution
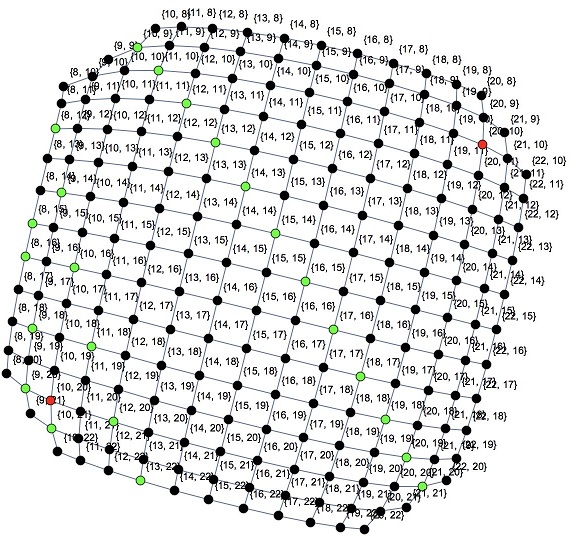
Consider the polynomial $f_{a,b}(x)=x^2+ax+b$ and its value at $x=-1:$ $f_{a,b}(-1)=b-a.$ Every time $a$ or $b$ changes by $\pm 1$ so does the expression $b-a.$ Now $f_{10,20}(-1)=11$ whereas $f_{20,10}(-1)=-9.$ Thus it follows that in the process of getting one from the other there ought to be a stage with $f_{a,b}(-1)=0,$ meaning that the integer $-1$ is the root of a provisional polynomial. The other root is naturally also an integer. The probability of this happening is $1.$
Graphical Illustration
The probability is $1,$ since you're forced to go through the diagonal where $b=c+1,$ which admits the roots $-1$ and $-c.$
Acknowledgment
This is problem 383 - a little modified - from a Russian collection of olympiad problems by N. B. Vasilyev and A. A. Egorov.
Konstantin Knop has kindly informed of additional details: the original problem (by A. A. Berzin'sh) was offered at the XVII All-Union Mathematical Olympiad for grade 8.
The illustration is by Marcos Carreira.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581617
