Clough's theorem: the simplest proof
What Might This Be About?
Explanation
GRÉGOIRE NICOLLIER
UNIVERSITY OF APPLIED SCIENCES OF WESTERN SWITZERLAND
ROUTE DU RAWYL 47, CH-1950 SION, SWITZERLAND
The following result was reportedly first noticed in 2003 by Duncan Clough, a high-school student experimenting with dynamic geometry [Villiers]. There are many proofs, using for example Cartesian coordinates or Viviani's theorem about the constant sum of the distances from a point to the sides of an equilateral triangle. The proof presented here is without any doubt the simplest and was proposed in the first round of the British Mathematical Olympiad 2013/14.
For an equilateral triangle $ABC$ and any point $P$ with orthogonal projections $D$ on $AB,$ $E$ on $BC,$ and $F$ on $CA,$
the sum of lengths $AD+BE +CF$ is the semiperimeter of $ABC.$
where $AD$ is negative when $\overrightarrow{AD}$ and $\overrightarrow{AB}$ have opposite directions and similarly for $BE$ and $CF.$
Proof
The assertion is obvious when P is the center O of ABC. One can go from O to any point P by moving first on an altitude and then on a parallel to another altitude.
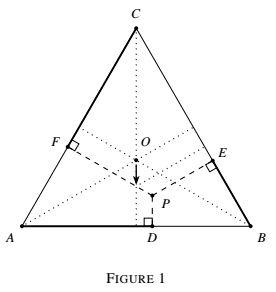
As easily seen in Figure 1, each such move leaves one of the lengths constant as well as the sum of the other two.
If $P$ lies inside $\Delta ABC,$ the parallels to the sides through $P$ delimit three parallelograms and three equilateral triangles inside $ABC$ and show at once that the sum of the areas
$[APD] + [BPE] + [CPF]$ is half $[ABC].$
References
- M. De Villiers, An illustration of the explanatory and discovery functions of proof, Pythagoras 33(3) (2012) Art. #193, 8 pages. https://dx.doi.org/10.4102/pythagoras.v33i3.193
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73570569
