When Is Triangle Isosceles:
Miguel Ochoa Sanchez's Criterion
Source

Problem
In $\Delta ABC,\;$ point $P\;$ is on the angle bisector $AD.\;$ $BP\;$ meets $AC\;$ in $E;\;$ $CP\;$ meets $AB\;$ in $F.$

Prove that if
$\displaystyle \frac{1}{AB^3}+\frac{1}{AE^3}=\frac{1}{AC^3}+\frac{1}{AF^3},$
the triangle is isosceles.
Lemma 1
Under the conditions of the above statement, if $AC\gt AB,\;$ then $[\Delta BCE]\gt [\Delta BCF],\;$ where $[X]\;$ denotes the area of shape $X.$
The lemma is equivalent to the assertion that point $E\;$ is "above" point $F.$
The lemma has an important consequence.
If $AC\gt AB,\;$ then
$AB\cdot AE\lt AC\cdot AF,$
Indeed, the lemma implies that
$\displaystyle\frac{1}{2}\sin A\cdot AB\cdot AE=[ABE]\lt [ACF]=\frac{1}{2}\sin A\cdot AC\cdot AF.$ Thus we have $AB\cdot AE\lt AC\cdot AF.$
Lemma 2
Under the conditions of the above statement,
$\displaystyle\frac{1}{AB}+\frac{1}{AE}=\frac{1}{AC}+\frac{1}{AF}.$
Indeed, by Ceva's theorem, $\displaystyle\frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1.\;$ In addition, using the fact that $AD\;$ is an angle bisector, $\displaystyle\frac{AB}{AC}=\frac{BD}{DC}.\;$ Combining the two we get,
$\displaystyle\frac{AB-AF}{AB\cdot AF}=\frac{AC-AE}{AC\cdot AE}.$
This reduces to the required identity.
The two lemmas combined give the following:
If $AC\gt AB,\;$ then
$AB+AE\lt AC+AF,$
Indeed, by Lemma 2, $\displaystyle\frac{AB+AE}{AB\cdot AE}=\frac{AC+AF}{AC\cdot AF}.\;$ So, since $AB\cdot AE\lt AC\cdot AF,\;$ so too $AB+AE\lt AC+AF.$
A Simplified Version
First we prove the following
In $\Delta ABC,\;$ point $P\;$ is on the angle bisector $AD.\;$ $BP\;$ meets $AC\;$ in $E;\;$ $CP\;$ meets $AB\;$ in $F.$

Prove that if
$\displaystyle \frac{1}{AB^2}+\frac{1}{AE^2}=\frac{1}{AC^2}+\frac{1}{AF^2},$
the triangle is isosceles.
The proof is by contradiction. WLOG, assume $AC\gt AB.\;$ Then, by Lemma 2
$\displaystyle\left(\frac{1}{AB}+\frac{1}{AE}\right)^2=\left(\frac{1}{AC}+\frac{1}{AF}\right)^2,$
implying, under our assumption, $\displaystyle\frac{2}{AB\cdot AE}=\frac{2}{AC\cdot AF}.$ But this contradicts Lemma 1.
Proof 1
We shall assume, as before, $AC\gt AB\;$ and now also $\displaystyle \frac{1}{AB^3}+\frac{1}{AE^3}=\frac{1}{AC^3}+\frac{1}{AF^3}.\;$ By Lemma 2,
$\displaystyle\left(\frac{1}{AB}+\frac{1}{AE}\right)^3=\left(\frac{1}{AC}+\frac{1}{AF}\right)^3,$
and subsequently,
$\displaystyle \frac{3}{AB\cdot AE\cdot (AB+AE)}=\frac{3}{AC\cdot AF\cdot (AC+AF)}.$
This is false by the corollaries to the two lemmas.
Proof 2
This is the original proof by Miguel Ochoa Sanchez.
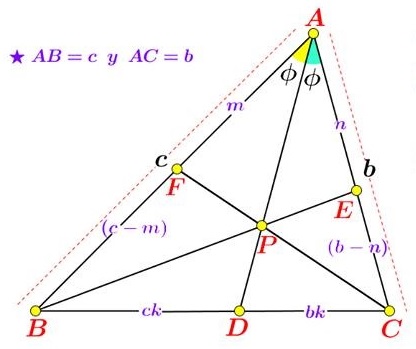

Proof 3
Denote $\displaystyle\frac{1}{AB}+\frac{1}{AE}=s,\;$ $\displaystyle\frac{1}{AB}\cdot \frac{1}{AE}=p,\;$ $\displaystyle\frac{1}{AC}+\frac{1}{AF}=q,\;$ $\displaystyle\frac{1}{AC}\cdot\frac{1}{AF}=r.\;$
In $\Delta ABE,\;$ $\displaystyle AP=\frac{2\cos\phi}{s}\;$ and in $\Delta ACF,\;$ $\displaystyle AP=\frac{2\cos\phi}{q},\;$ implying $q=s.\;$ The given condittion is equivalent to $s^3-3sp=s^3-3sr\;$ such that $r=p.\;$ From here
$\displaystyle\left\{\frac{1}{AB},\frac{1}{AE}\right\}=\left\{\frac{1}{AC},\frac{1}{AF}\right\}.$
There are two possibilities: $AB=AF,\;AC=AE\;$ or $AB=AC,\;AE=AF.\;$ The former may only hold when $P=D,\;$ in which case the condtion of the problem becomes an inconsequential tautology and needs to be excluded. The latter possibility confirms the conclusion of the problem.
Extra Challenge
In $\Delta ABC,\;$ point $P\;$ is on the angle bisector $AD.\;$ $BP\;$ meets $AC\;$ in $E;\;$ $CP\;$ meets $AB\;$ in $F.$

Prove that if
$\displaystyle \frac{1}{AB^4}+\frac{1}{AE^4}=\frac{1}{AC^4}+\frac{1}{AF^4},$
the triangle is isosceles.
Think of other exponents.
Answer to the Extra Challenge
As in Proof 3, $q=s.\;$ From the given condition, $s^4-4s^2p+2p^2=s^4-4s^2r+2r^2,\;$ implying $4s^2p-2p^2=4s^2r-2r^2.\;$ But $\displaystyle 0\lt p,r\lt\frac{s^2}{4}\;$ and the quadratic $f(x)=x^2-2s^2x\;$ is injectivebon $[0,s^2]\;$ such that $r=p.\;$ The ending as in Proof 3.
Acknowledgment
The problem above has been posted by Miguel Ochoa Sanchez at the Peru Geometrico facebook page. Proof 2 is by Miguel; Proof 3 and the resoponse to the Extra Challenge is by Leo Giugiuc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573773
