Sanchez' Viviani's Area Analogue
What Might This Be About?
Source
The following has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page:
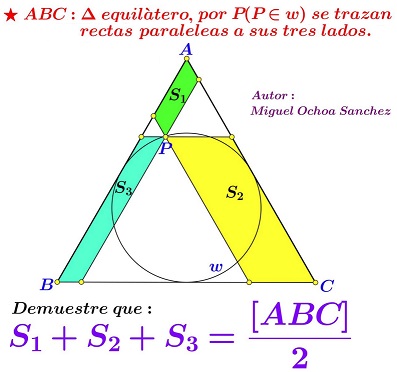
Problem
I find it more convenient to deal with an equivalent problem:
Point $P$ lies on the incircle of an equilateral $\Delta ABC.$ Three lines through $P$ parallel to the sides, divide the triangles into three parallelograms, and three smaller equilateral triangles, say, $T_1,$ $T_2,$ $T_3:$
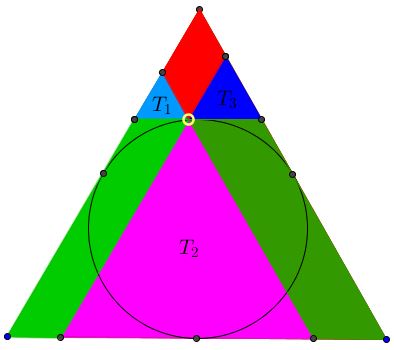
If $[F]$ denotes the area of shape $F,$ prove that
$[ABC]=2([T_1]+ [T_2]+[T_3]).$
Solution
The proof uses basic analytic geometry. Assume $h,$ $h_1,$ $h_2,$ $h_3$ are the lengths of the altitudes of the four triangles involved. The problem is equivalent to showing that
$h^2=2(h_1^2+h_2^2+h_3^2).$
Without loss of generality, assume also that the inradius of $\Delta ABC$ equals $1$ and that the vertices are located as follows: $A=(0,2),$ $B=(-\sqrt{3},-1),$ $C=(\sqrt{3},-1).$ (This in particular means that $h=3$ and, say, $AB=2\sqrt{3}).$ Assume also that $P$ is located at the top third of the incircle, $P=(\cos\alpha ,\sin\alpha ).$
Obviously, $h_2=1+\sin\alpha.$ To determine $h_1$ and $h_3$ recollect that the distance from point $X=(u,v)$ to the line $\ell:\;ax+by+c=0\;$ can be found from
$\displaystyle dist(X,\ell)=\frac{|au+bv+c|}{\sqrt{a^2+b^2}}.$
The two sidelines of $\Delta ABC$ are easy to find: $\pm\sqrt{3}x+y-2=0.\;$ Accordingly, $\displaystyle h_1=\frac{1}{2}|-\sqrt{3}\cos\alpha+\sin\alpha-2|\;$ and $\displaystyle h_3=\frac{1}{2}|\sqrt{3}\cos\alpha+\sin\alpha-2|.\;$ Now we check
$\displaystyle\begin{align} h_1^2+h_2^2+h_3^2 &= (1+\sin\alpha )^2\\&\;\;\;+\frac{1}{4}(-\sqrt{3}\cos\alpha+\sin\alpha-2)^2+\frac{1}{4}(\sqrt{3}\cos\alpha+\sin\alpha-2)^2\\ &=\frac{1}{4}[(4+8\sin\alpha+4\sin^2\alpha)+(6\cos^2\alpha+2\sin^2\alpha+8-8\sin\alpha)]\\ &=\frac{1}{4}[12+6(\sin^2\alpha+\cos^2\alpha)]\\ &=\frac{9}{2}=\frac{h^2}{2}. \end{align}$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575245
