An Unexpected Rhombus
What is this about?
Problem
Given a pair of circles , $(A)$ and $(B)$, not containing each other's centers. From the center of each draw tangents to the other: $BL,$ $BG$ and $AK,$ $AH.$ The four straight lines intersect the circles in four additional points: $(A)$ in points $E$ and $F,$ and $(B)$ in $I$ and $J.$ The extended chords $JK,$ $EL,$ $FG,$ and $HI$ form a quadrilateral $MONP.$
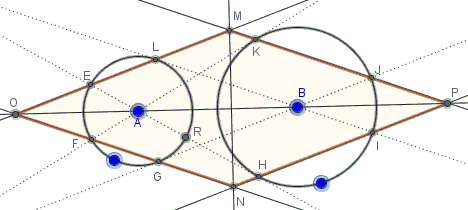
Prove that $MONP$ is a rhombus.
Hint
Watch for tangencies, right triangles, equal angles.
Solution
Let $U$ be the intersection of $AH$ and $BL.$ Denote $\angle AUB=\alpha.$
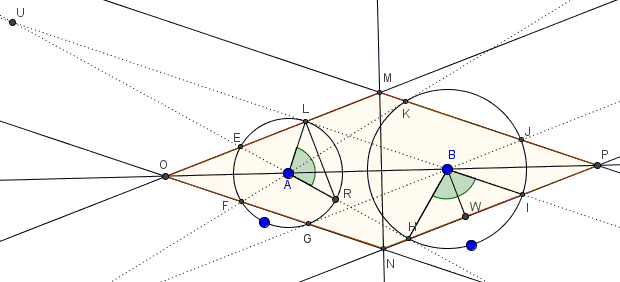
Right triangles $ALU$ and $BHU$ are similar, making both angles $UAL$ and $UBH$ equal to $90^{\circ}-\alpha.$ It follows that $\angle ALR=\angle HBI=90^{\circ}+\alpha,$ as supplementary to angles $UAL$ and $UBH,$ respectively.
Note that triangles $ALR$ and $BHI$ are isosceles. If $W$ is the midpoint of $HI$ then $\angle IBW=(90^{\circ}+\alpha)/2.$ On the other hand, since $\Delta ALR$ is also isosceles,
$ \begin{align} \angle BLR &= \angle ALB - \angle ALR \\ &=90^{\circ}-(90^{\circ}-\alpha)/2 \\ &=(90^{\circ}+\alpha)/2. \end{align} $
We conclude that $LR\parallel BW$ but one is perpendicular to $MO,$ the other to $NP$ such that $MO\parallel NP.$ Similarly, $ON\parallel MP,$ implying that $MONP$ is a parallelogram. However, by symmetry, $MP=NP$ and $MO=NO,$ which proves that $MONP$ is indeed a rhombus, as required.
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574867
