Two Similar Triangles with Parallel Sides

What is this about?

Problem

Let there be two similar triangles $\Delta A_{1}B_{1}C_{1}$ and $\Delta A_{2}B_{2}C_{2}$ with the corresponding sides parallel: $A_{1}B_{1}\parallel A_{2}B_{2},$ etc. Let $r$ be a real number. Define six points $rA_{1}+(1-r)B_{2},$ $rA_{1}+(1-r)C_{2},$ $rB_{1}+(1-r)A_{2},$ $rB_{1}+(1-r)C_{2},$ $rC_{1}+(1-r)A_{2},$ and $rC_{1}+(1-r)B_{2}.$

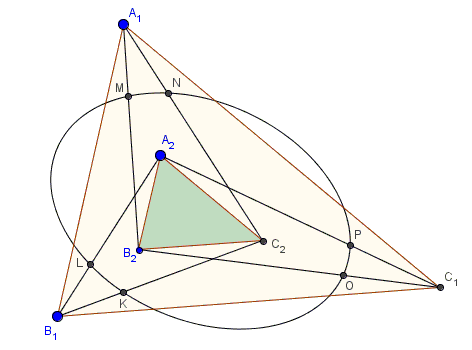
Two similar triangles with parallel sides and a conic

Prove that the six points lie on a conic.

Hint

Pay attention to what kind of hexagon is formed by the six points.

Solution

The opposite sides of the hexagon so obtained are parallel:

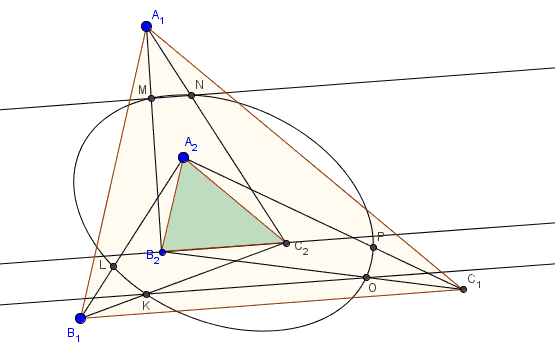
Two similar triangles with parallel sides and a conic - solition

Thus, we are in a position to apply the statement about a hexagon formed by three pairs of parallel lines: the six points are conconical. However, unlike in the general case, in the current problem the conic is always bounded, making it an ellipse.

Acknowledgment

Dao Thanh Oai has posted the problem with $r=.5$ at the CutTheKnotMath facebook page, pointing out the difference with the general case.

71547325