Areas between Two Parallelograms
What Might This Be About?
Problem
A smaller parallelogram $OA'B'C'\;$ is inside a larger parallelogram $OABC\;$ such that they share a common vertex $O\;$ along with two of their adjacent edges as shown in the figure. $A'B'\;$ and $C'B'\;$ are produced to meet the edges of the outer parallelogram at $P\;$ and $Q\;$ respectively.
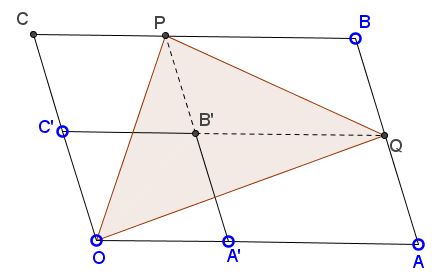
Show that the area of the triangle $OPQ\;$ is half that of the $L-shaped\;$ region between the two parallelograms.
Solution
Let $[F]\;$ denote the area of shape $F.\;$ Then
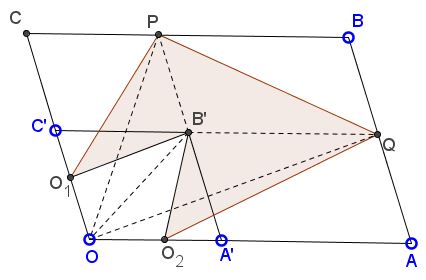
By Euclid I.37,
$\begin{align} [\Delta B'OP]&=[\Delta B'O_1P]=[\Delta B'C'P]=\frac{1}{2}[C'B'PC] \\ \; [\Delta B'OQ]&=[\Delta B'O_2Q]=[\Delta B'A'Q]=\frac{1}{2}[A'AQB'] \\ \; [\Delta PB'Q]&=\frac{1}{2}[B'QBP], \end{align}$
But then
$\begin{align} [\Delta POQ]&=[\Delta B'OP]+[\Delta B'OQ]+[\Delta PB'Q]\\ &=[\Delta B'C'P]+[\Delta B'A'Q]+[\Delta PB'Q]\\ &=\frac{1}{2}([C'B'PC]+[A'AQB']+[B'QBP]). \end{align}$
Acknowledgment
The statement has been communicated to me by G. S. Ranganath, with the solution by his son G. R. Jayanth.
Extra
Here's a related problem from an upcoming book Population Explosion and Other Mathematical Puzzles (World Scientific, 2016) by Dick Hess.
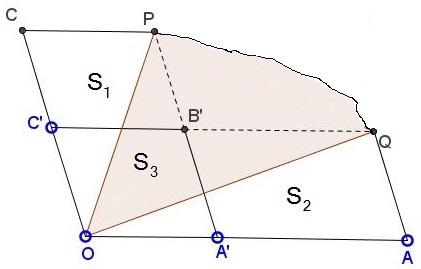
The figure below show a lake $OA'AQPCC'\;$ That is nearly a parallelogram except for a segment of its shore line. Let $S_1=[CC'QP],\;$ $S_2=[A'AQP],\;$ and $S_3=[OPQ].\;$ Express $S_3\;$ in terms of $S_1\;$ and $S_2.$
Answer: 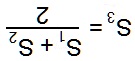
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574964
