Cutting Circle to Rearrange Two Dots

Problem

In addition to the center of a circle another dot is marked within. Cut the circle into at most three parts such that, by rearranging the pieces, you get a circle with the center at the dot.

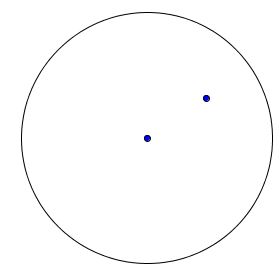
a dot in the circle - problem

Solution 1

A three pieces solution: Cut off equal circles - small enough to fit within the circle - around the center and the given dot. Exchange the two small circles.

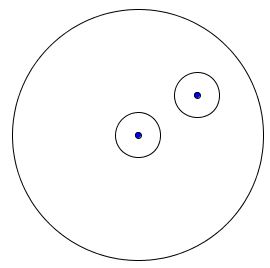
a dot in the circle - solution 1

Solution 2

A two pieces solution: Draw equal circles - small enough to fit within the circle - around the center and the given dot. Draw the common external tangents to the two circle. Cut off so obtained shape, turn it around and fit it back in.

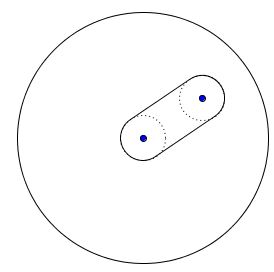
a dot in the circle - solution 2

Solution 3

Around the given dot draw a circle (an arc actually) with the radius of the given circle. Cut along the arc. The given circle will be split into a lens-like and a crescent-like shapes. Slider the latter around the lens.

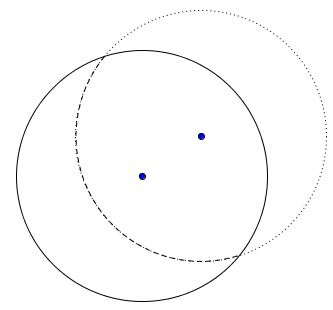
a dot in the circle - solution 3

References

S. Dorichenko, A Moscow Math Circle: Week-by-week Problem Sets, MSRI/AMS, 2012, #0.4

Generalization

What if both of the given points are marked randomly in the circle? How many cuts does it take to exchange the two points?

a dot in the circle - problem 2

The first two solutions will clearly work in this case as well. What about the third solution? Can the third solution be modified to solve the more general problem?

72202385