Two Circles, Tangents and Two Collinearities
What Might This Be About?
Problem
Point $O$ is outside two given circles $(O_1)$ and $(O_2).$ $OK,$ $OG$ are tangent to $(O_1);$ $OM,$ $ON$ are tangent to $(O_2).$ $IP$ is a common tangent of $(O_1),$ $(O_2).$ Assume that $IK$ meets $PN$ at $C;$ $IG$ meets $PN$ at $A,$ $PM$ meets $IG$ at $B;$ $IK$ meets $MP$ at $D.$
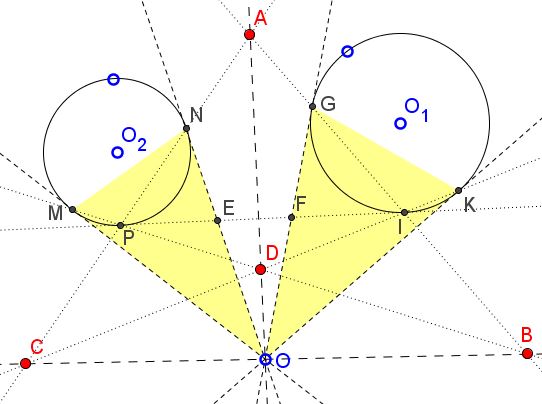
Prove that $B,$ $O,$ $C$ are collinear, and so are $O,$ $A,$ $D.$
Solution
Let $X$ be the intersection of $IO$ and $(O_{1});$ $Y$ the intersection of $PO$ and $(O_{2}).$ Since $PNYM$ and $IKXG$ are both harmonic quadrilaterals, $(PI,PY;\,PM,PN)=-1=(IP,IX;\,IG,IK),\,\,$ i.e., the pencils $P(I,\,Y,\,M,\,N)=(PI,\,PY,\,PM,\,PN)\,$ and $I(P,\,X,\,K,\,G)=(IP,\,IX,\,IG,\,IK)\,$ are perspective, implying the intersection of $PY$ and $IX,$ $PM\,$ and $IG,$ $PN\,$ and $IK\,$ are collinear, i.e., $O,\,B,\,C\,$ are collinear.
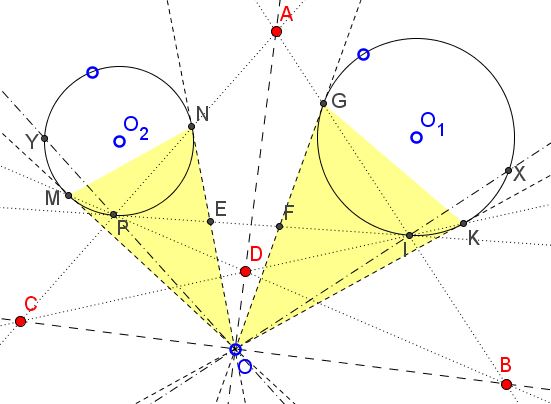
If the cross-ratio $(\alpha,\beta;\,\gamma,\delta)=r,$ then $(\alpha,\beta;\,\delta,\gamma)=1/r,\,$ so that if $r=-1$ both are harmonic. In our case, $-1=(IP,IX;\,IG,IK)=(IP,IX;\,IK,IG)$ and the same logic, as above, makes the pencils $P(I,\,Y,\,M,\,N)=(PI,\,PY,\,PM,\,PN)\,$ and $I(P,\,X,\,K,\,G)=(IP,\,IX,\,IK,\,IG)\,$ perspective, so that $O,\,A,\,D\,$ are also collinear.
Q.E.D
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. Dao has later posted a solution by Telv Cohl, reproduced above.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73568970
