Triangle in a 4x4 Square

Problem

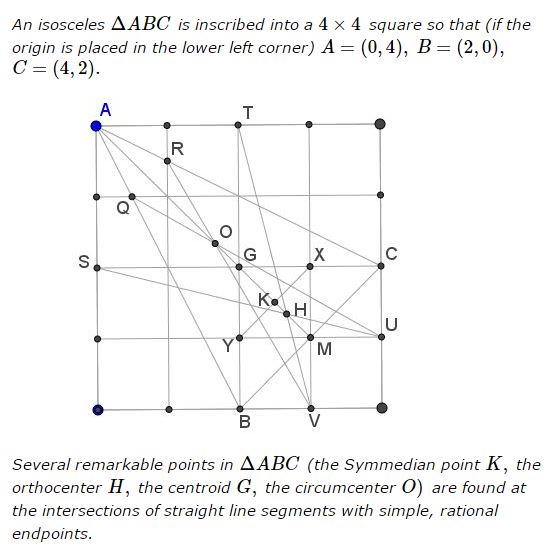
Triangle in a 4x4 Square>
</p>
</div>

<h3>Symmedian Point $K$</h3>
<div>
<div class=

The Symmedian point $K\,$ is the center of the square $MXYG.$

The Symmedian point of an isosceles triangle inscribed into a 4x4 square

In the diagram, $G=(2,2)\,$ and $M=(3,1).\,$ The center of the segment $GM,\,$ say, $Z=\displaystyle\left(\frac{5}{2},\frac{3}{2}\right).\,$

On the other hand, obviously, $a^2=8,\,$ $b^2=c^2=20.\,$ In the barycentric coordinates, $K=a^2:b^2:c^2,\,$ so that

$\displaystyle\begin{align} K&=\frac{a^2A+b^2B+c^2C}{a^2+b^2+c^2}\\ &=\frac{1}{48}[8(0,4)+20(2,0)+20(4,2)]\\ &=\left(\frac{5}{2},\frac{3}{2}\right), \end{align}$

which is exactly the center $Z\,$ of the square $MXYG.$

Centroid $G$

The centroid $G\,$ is the center of the ambient square

The centroid of an isosceles triangle inscribed into a 4x4 square

$\displaystyle G=\frac{A+B+C}{3}=\frac{(0,4)+(2,0)+(4,2)}{3}=\frac{(6,6)}{3}=(2,2).$

Circumcenter $O$

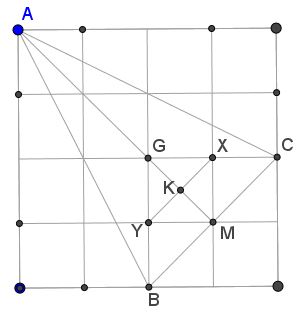
The circumcenter $O\,$ is the intersection $O=RV\cap QU\,$

The circumcenter point of an isosceles triangle inscribed into a 4x4 square

We have extra points: $R=\left(1,\frac{7}{2}\right),\,$ $V=(3,0),\,$ $Q=\left(\frac{1}{2},3\right),\,$ and $U=(4,1).\,$ Clearly, $O\,$ is one the line $AM:\;y=4-x.\,$ Since $AO=BO,\,$ $2x^2=(x-2)^2+(x-4)^2,\,$ so that $x=\displaystyle\frac{5}{3},\,$ and, therefore $O=\displaystyle\left(\frac{5}{3},\frac{7}{3}\right).$

Now to check that $R,O,V\,$ are collinear, verify that

$\left|\begin{array}{ccc}\,2&7&2\\5&7&3\\3&0&1\end{array}\right|=0.$

Similarly, $Q,O,U\,$ are also collinear.

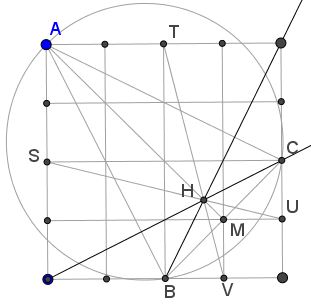
Orthocenter $H$

The orthocenter $H\,$ is the intersection $H=TV\cap SU.$

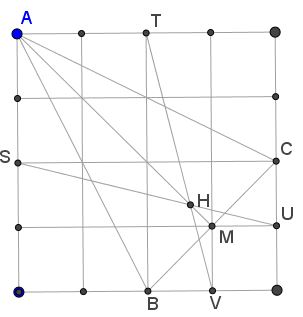
The orthocenter of an isosceles triangle inscribed into a 4x4 square

From $G=\displaystyle\frac{2\cdot O+H}{3},\,$ $H=\displaystyle\left(\frac{8}{3},\frac{4}{3}\right).\,$ Now, $T,O,V\,$ a collinear, because

$\left|\begin{array}{ccc}\,2&4&1\\8&4&3\\3&0&1\end{array}\right|=0.$

Similarly we verify that $S,O,U\,$ are also collinear.

As an extra, we may consider the following diagram:

The orthocenter of an isosceles triangle inscribed into a 4x4 square, second variant

Acknowledgment

The problem is a combination of several posts by Tran Quang Hung at the CuTheKnotMath facebook page with solutions by Leo Giugiuc.