Triangle in a 5x5 Square
Source
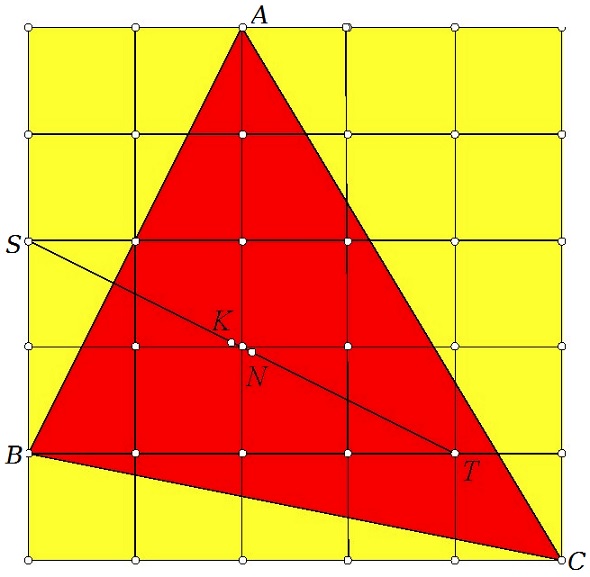
Problem
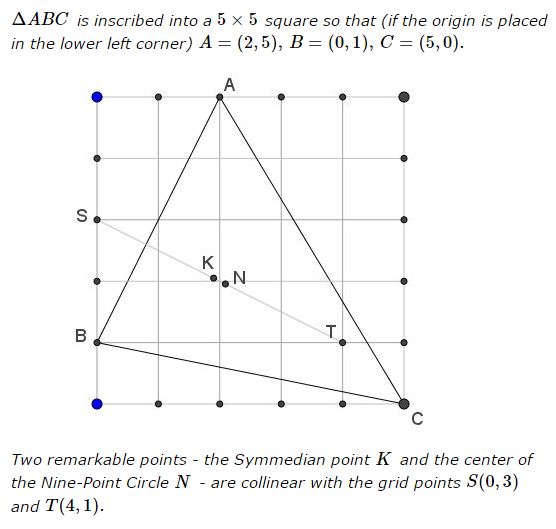
Symmedian Point $K$
Obviously, $a^2=26,\,$ $b^2=34,\,$ $c^2=20.\,$ In the barycentric coordinates, $K=a^2:b^2:c^2,\,$ so that
$\displaystyle\begin{align} K&=\frac{a^2A+b^2B+c^2C}{a^2+b^2+c^2}\\ &=\frac{1}{80}[26(2,5)+34(0,1)+20(5,0)]\\ &=\left(\frac{38}{20},\frac{41}{20}\right). \end{align}$
To check that $K\in ST\,$ we apply the condition of collinearity:
$\left|\begin{array}{ccc}\,0&3&1\\4&1&1\\38&41&20\end{array}\right|=\left|\begin{array}{ccc}\,0&3&1\\4&-2&0\\38&-19&0\end{array}\right|=4(-19)-38(-2)=0.$
Nine-Point Center $N$
We know that $N\,$ is the midpoint between the orthocenter $H\,$ and the circumcenter $O:\;$ $\displaystyle N=\frac{H+O}{2}.\,$ Thus we are going to determine the coordinates of these two points first:
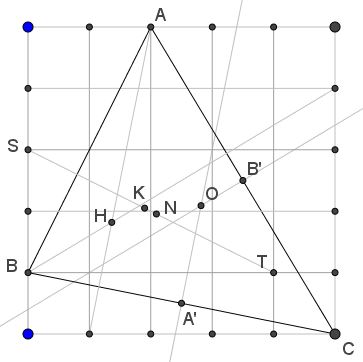
The altitudes from $A\,$ and $B\,$ have equations $y=5(x-1)\,$ and $\displaystyle y=\frac{3}{5}x+1\,$ solving which we obtain $H=\displaystyle\left(\frac{15}{11},\frac{20}{11}\right).$
The perpendicular bisectors of $AC\,$ and $BC\,$ are defined by the two equations $y=\displaystyle\frac{3}{5}x+\frac{2}{5}\,$ and $y=5x-12\,$ solving which we obtain $O=\displaystyle\left(\frac{31}{11},\frac{23}{11}\right).\,$ The midpoint of $HO\,$ then equals $N=\displaystyle\left(\frac{46}{22},\frac{43}{22}\right)\,$ and this is collinear with $S\,$ and $T:$
$\left|\begin{array}{ccc}\,0&3&1\\4&1&1\\46&43&22\end{array}\right|=\left|\begin{array}{ccc}\,0&3&1\\4&-2&0\\46&-23&0\end{array}\right|=4(-23)-46(-2)=0.$
Acknowledgment
The problem has been kindly posted by Tran Quang Hung at the CuTheKnotMath facebook page.
|Contact| |front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73607691
